この前はTensorFlowをインストールして満足しました。
まずは基本的からニューラルネットワークをやってみることにします。
ニューラルネットワークの理論
ディープラーニングやってみたいとは言ったものの、ニューラルネットもさっぱりわかんないので、 はじめはニューラルネットワークの勉強から。
参考にしたのはこちらです。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
- 作者: 斎藤康毅
- 出版社/メーカー: オライリージャパン
- 発売日: 2016/09/24
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (18件) を見る
こちらの本は理系出身の私には非常に分かりやすかったのです。 ただ数式がバンバン出て来るので簡単な線形代数や線形代数とニューラルネットワークの関連がつかめないと難しいらしいです。
この記事では、難しい理論は最小限にして、ニューラルネットワークでなにをやっているのかを書きます。 細かい話は本を読んで下さいってことで。笑
全体像
まずよくあるニューラルネットワークの模式図がこちら。
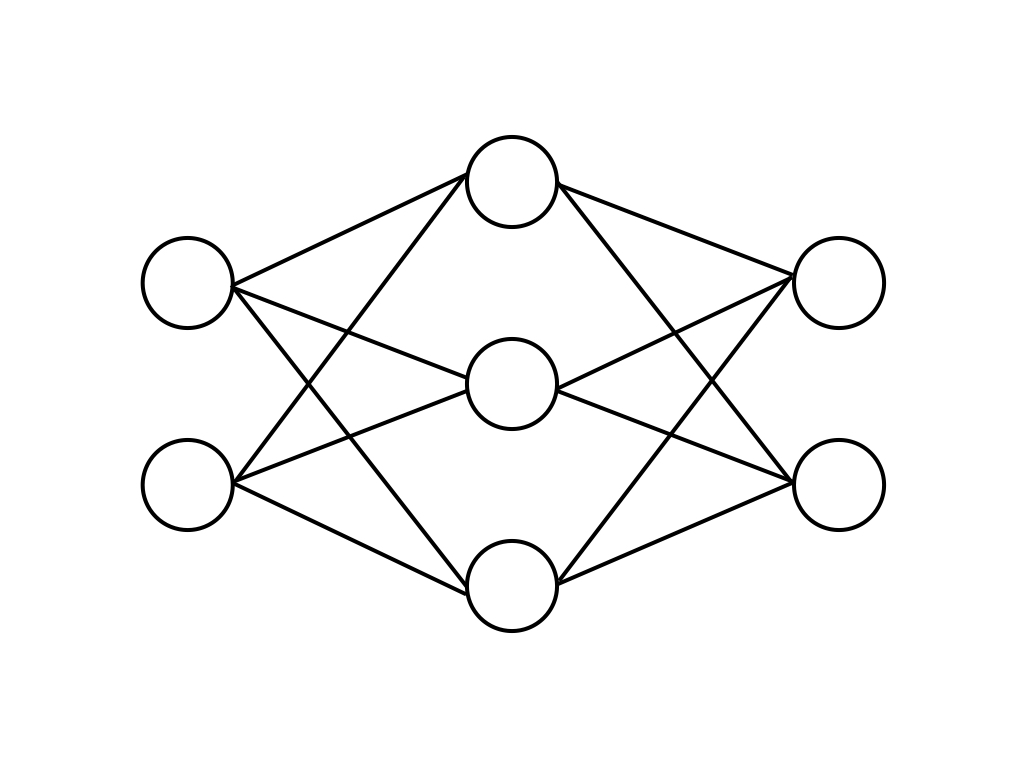
見方としては、左から右に向かって電気信号が伝播することを意味しており、左から「入力層」「中間層」「出力層」といいます。 イメージとしてはこんな感じ。

基本的には、この「左から右」の方向に向かって機械学習したいことをモデル化していきます。 また、人間の脳は「学習」が可能であり、ニューラルネットワークでは、「学習」もモデル化しています。 そのため、処理の流れとしてはこんな感じです。

なので、全体のイメージはこんな感じ。

この動作がひたすらぐるぐる回るのがニューラルネットワークってやつです。
パーセプトロン
ちょっとずつ細かい部分について見ていきます。 注目する範囲はこちらです。

こちらを拡大すると、こんな感じになります。

こちらはパーセプトロンと呼ばれニューラルネットワークの一番小さい単位になっています。 こいつは、「左のノード(◯)の値をリンク(→)の重みをかけ合わせて足し合わせた値が右のノード(◯)の値になる」 という単純な仕組みになっています。
これくらい小さいスケールだと簡単なのですが、こんなサイズだとどうでしょう?

ちょっとコーディングするのが嫌になってきますね。 ここで、行列を使って簡単に表現します。 入力をベクトル、入力-出力のそれぞれのリンクの重みを行列にしたベクトルと行列の内積で表現するとこんな感じになります。
こんなにスッキリしちゃいます。実際にはもう少しごちゃごちゃするんですが、それでも一行で表現できます。 pythonをはじめ、そのへんのプログラミング言語には行列計算ライブラリが用意されているので、ベクトル/行列をセットするだけでスッキリ記述できますし、めっちゃ速く計算してくれます。
活性化関数
ニューラルネットワークでは入力の総和がそのまま出力されるわけではなく、「活性化関数」によって「発火」します。 これは、生物の神経細胞にも同じことが起こっているようで、どうでもいいような微弱な刺激は次の神経細胞に伝達しないようになっているようです。

活性化関数を表現するのに広く使用されるのが、シグモイド関数とReLU関数です。
シグモイド関数

ReLU関数

このような関数を噛ませることで、発火を表現しています。 とりあえずこんなのがワンクッション入っているんだーくらいで大丈夫です。 ここまでのパーセプトロンと活性化関数さえ分かれば、「右方向の伝達」は実装できます。
学習
パーセプトロンのところで出てきたリンクの重みですが、この値次第で出力層の結果が変化します。 そのため、このリンクの重みを適切な値に調整する作業をニューラルネットワークでは「学習」と呼びます。
下の図では、「ニューラルネットワークの出力」と「答え」を図示しています。

棒グラフが出力値、星が実際の答えを表しており、図のようにギャップが生じます。
学習では、推定した値と理想の解答との差分(損失関数)を求めます。 損失関数の値をもとに、リンクの重みを調整していきます。

算出された損失関数をもとに、「本来出力はどうなって欲しいのか」が分かるので、その方向に予想が近づくようにリンクの重みを調整します。 これをさまざまな入力(たくさんの画像、いろんなバリエーションの音声など)に対して行い、学習を繰り返すことで予想の精度を上げていきます。
誤差逆伝播法(Back propagation)
さて、学習では重みに関する微分Δwを計算する必要がありました。 高校レベルの
みたいな関数ならなんてことはないんですが、ニューラルネットワークだと、
- 活性化関数が機能している
- 層の数が多い(10層とかになる場合もある)
なんて理由から、微分求める事自体が簡単ではありません。 そのため、学習時の微分を効率的に実装することがニューラルネットワークの一つの鍵になってきます。
現在広く使用されている手法として、誤差逆伝播法(Back propagation)と呼ばれる方法があります。 イメージとしてはこちら。

上の図では、下のような式をグラフ構造で示しています。
入力a,b,cがに対する出力yが分かった時、上の式を全微分すると
図で表すとこんな感じ。

損失関数が分かるとdyの値がわかるので、あとはリンクの重みが該当する変数の項の係数分だけ元の関数を修正すれば学習を表現できます。
ニューラルネットワークでは行列が使用されるので、行列で表現された形にするとこんな感じ。

上の図では、Wが学習で該当する変数(行列)なのでこれ以外の項は全てなくなります。 学習時の行列の微分や活性化関数の微分は、行列の内積なら微分はこれ、シグモイド関数を使った活性化関数は微分はこれ…みたいに、昔の偉い人が考えてくれた式があるので、そちらに代入していきます。 細かいところは本をご参照下さい。
層が多くなってもやることは一緒で、予測の時と逆の順番で微分を求めていき、各層のリンクの重みの修正値を求めていきます。

こんな感じのことをプログラムで実装すると、パラメータ調整を自動でやってくれるニューラルネットワークが出来上がりです。 勉強になります。。。
ニューラルネットワークの実装
自分で手書きで実装しようかと思ったのですが、著者の方が書いてくださったものがありますのでそちらをご参照下さい。
図をいっぱい作ってたら疲れちゃったので、実装は別の機会ということで。笑