Re:ゼロから始めるML生活

どちらかといえばエミリア派です

【R】時系列分析の覚書(基本、ウィナーフィルタ)

R 時系列分析

前回に引き続き、こちらの本をやっていきます。

基礎からわかる時系列分析 ―Rで実践するカルマンフィルタ・MCMC・粒子フィルター (Data Science Library)

基礎からわかる時系列分析 ―Rで実践するカルマンフィルタ・MCMC・粒子フィルター (Data Science Library)

前回は導入ということで、簡単な分析をなぞってみました。

tsunotsuno.hatenablog.com

今回の範囲はこちらです。

f:id:nogawanogawa:20180715133812j:plain:w500

前回はとりあえず簡単な時系列分析をやってみるといった位置づけでしたが、今回は状態空間モデルの基本をやってみます。

状態空間モデル

時系列データがどんな関係性にあるかを表現する際に、潜在変数があるかないかで大きく二分されます。 潜在変数を使用するモデルの一つが状態空間モデルで、逆に潜在変数を使用せず観測されるデータの関係性を直接表現するモデルの一つとしてARMAモデルが挙げられます。

状態空間モデルを図で示すと下のようになります。

f:id:nogawanogawa:20180721091602j:plain:w500

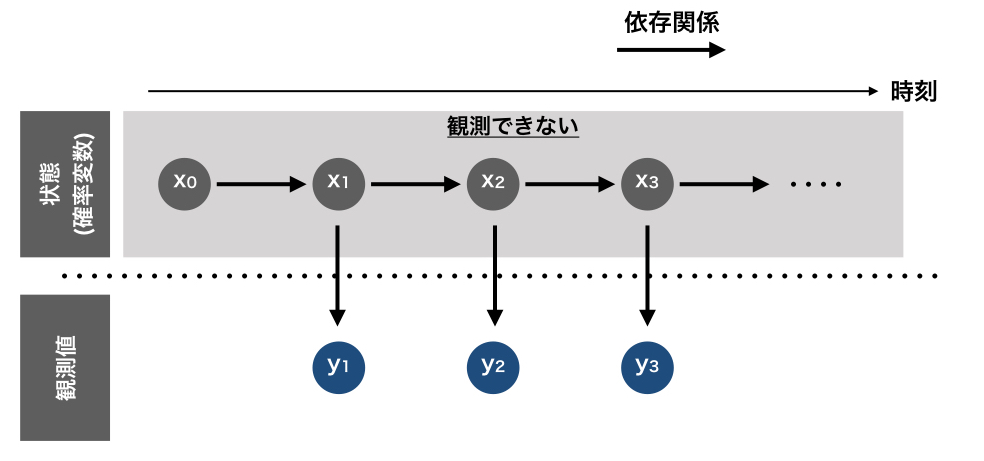
一方でARMAモデルを図にするとこんなイメージです。

f:id:nogawanogawa:20180908170953j:plain:w400

観測されるデータが何に依存しているかが最大の違いとなっています。

この本では状態空間モデルは次のように説明されています。

状態空間モデルは互いに関連のある系列的なデータを確立的に捉えるモデルの１つです。

確率空間モデルでは、直接観測されるデータ（観測値）と直接には観測されない確率変数（状態）を用います。 観測値や状態には、分析を行う上で解釈が容易になるように量を選ぶ必要があります。 そこで、ざっくり言うと下記のような関係性を仮定します。

状態については、状態は前時点のみに依存する（マルコフ性）
観測値については、ある時点の観測値についてはその時点の状態にのみ依存する

これとは対象的に、観測される時系列データだけを見て関係性を求めるモデルをARMAモデルと言ったりします。

状態空間モデルを確率分布で表現すると以下のようになります。

p(x_t | x_{0:t-1}, y_{1:t-1}) = p(x_t | x_{t-1})
p(y_t | x_{0:t}, y_{1:t-1}) = p(y_t | x_{t})

方程式で表すとこんな感じです。

x_t = f(x_{t-1}, w_t) (状態方程式、システム方程式)
y_t = h(x_t, v_t) (観測方程式)

wとvのことを、それぞれ状態雑音(システム雑音)と観測雑音と言います。

ちなみに、図でも確率分布でも方程式でも意味はすべて同じです。

状態の推定

状態空間モデルでの状態を推定することを考えます。

観測値は取得可能ですが、状態は観測不可能です。 そのため、分析に使用する際には、状態を推定することがポイントになります。

フィルタリング(現在の状態の推定)

フィルタリングは過去から現在まで観測された時系列データを使用して、現在の状態を推定します。

  • input : 観測された時系列データ
  • output : 現在の状態

イメージにするとこんな感じです。

f:id:nogawanogawa:20180721143132j:plain:w500

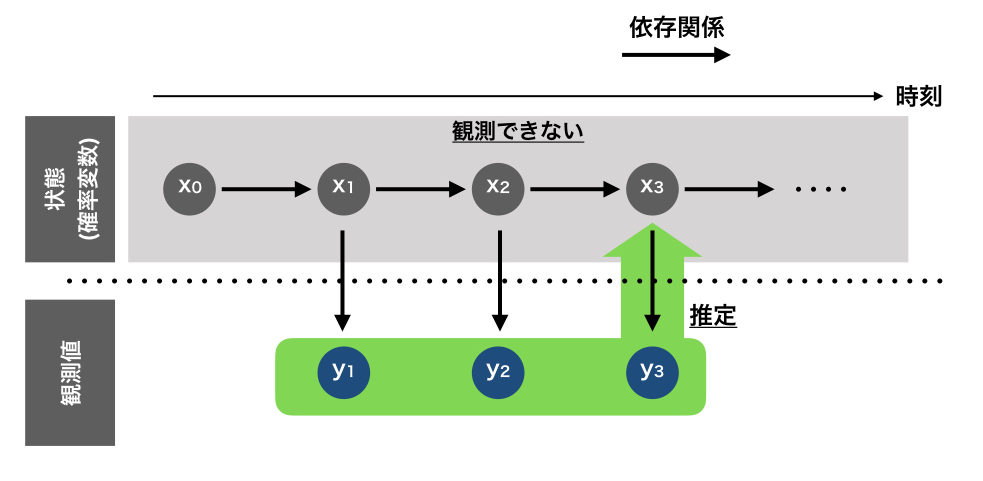
見方を変えるとこんな感じで表現されます。

f:id:nogawanogawa:20180721143109j:plain:w500

これは右方向が潜在変数の時間進行、下方向が観測値の時間進行を表しています。 実際には同じ時間軸に乗っているので、右下の方向に向かって進んでいきます。

フィルタリング分布について細かい数式はおいておいて、結論だけ書くと、

フィルタリング分布: p(x_t | y_{1:t}) = p(x_t | y_{1:t-1}) \frac{p(y_t | x_t}{p(y_t | y_{1:t-1})})

一期先予測分布: p(x_t | y_{1:t-1}) = \int p(x_t | y_{1:t-1}) p(x_{t-1} | y_{1:t-1}) dx_{t-1}

一期先予測尤度: p(y_t | y_{1:t-1}) = \int p(y_t | x_t) p(x_t | y_{1:t-1}) dx_t

となります。（証明は端折ります。本買って読んでください。）

簡単にまとめると、

フィルタリングでは時刻0の状態から始まり、

  1. 潜在変数が時間進行
  2. 潜在変数の変化に伴い観測値が変化

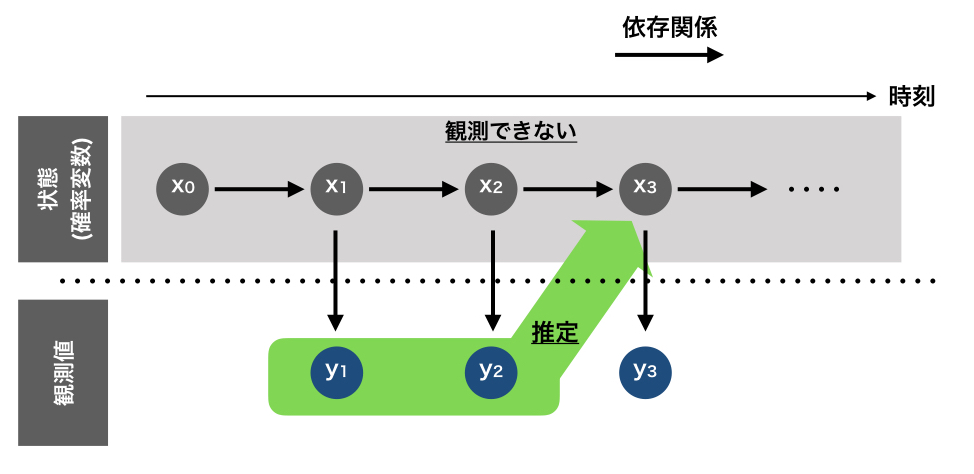
を繰り返していきます。イメージとしてはこんな感じです。

f:id:nogawanogawa:20180721143149j:plain:w500

このようにフィルタリングでは階段状に、現在の観測値から潜在変数を推定していきます。

予測(未来の状態を推定する)

次に未来の観測値について考えます。 未来なので観測値は手にはいりません。

f:id:nogawanogawa:20180721143209j:plain:w500

この場合は、手に入っている現在の観測値から潜在変数を求めていきます。（証明は端折ります。本買って読んでください。）

予測分布： p(x_{t+k} | y_{1:t}) = \int p(x_{t+k} | x_{t+k-1}) p(x_{t+k-1} | y_{1:t}) dx_{t+k-1}

イメージはこんな感じで潜在変数だけ時間進行するイメージで潜在変数を推定します。

f:id:nogawanogawa:20180721143221j:plain:w500

平滑化(過去の状態を推定する)

今度は現在より過去の状態を推定することを考えます。

f:id:nogawanogawa:20180721143236j:plain:w500

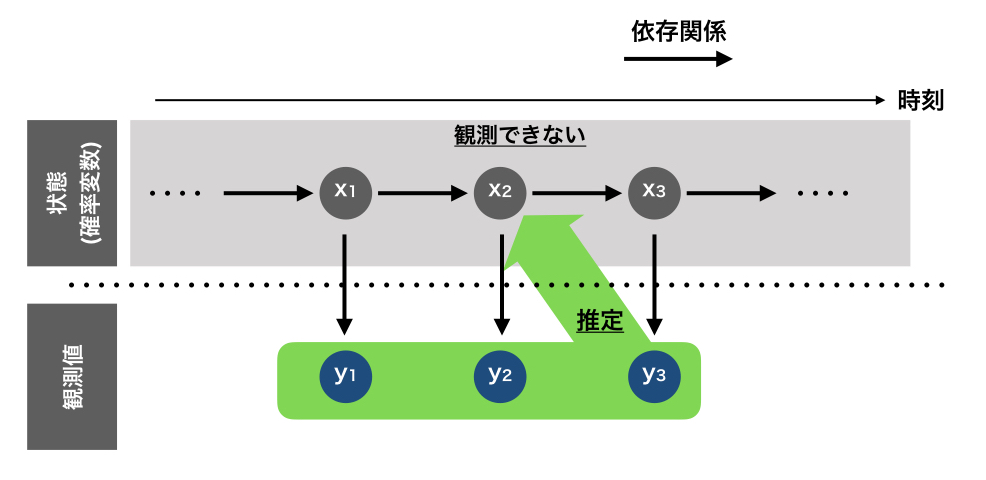
一旦時刻T（＞ｔ）までフィルタリングが完了している状態から考えます。 平滑化分布は下記のように表現されます。（証明は端折ります。本買って読んでください。）

平滑化分布: p(x_t | y_{1:T}) = p(x_t | y_{1:t}) \int\frac{p(x_{t+1} | x_t}{p(x_t+1 | y_{1:t})} p(x_{t+1} | y_{1:T})dx_{t+1}

これにより過去に遡って潜在変数を推定します。

f:id:nogawanogawa:20180721143248j:plain:w500

一括解法

ここからは実際に潜在変数を求めてみます。 まずは過去から知りたい時点までの状態を一括で求める一括解法についてです。

定常な状態時系列（平均・分散・自己共分散・自己相関係数が時間によって変化しない）に対して適用できるウィナーフィルタを見ていきます。

ウィナーフィルタ

下のような観測値と推定値の関係を考えます。

f:id:nogawanogawa:20180915100207j:plain:w500

そして、観測値から状態を推定する逆変換を下のように考えます。

f:id:nogawanogawa:20180915100230j:plain:w500

ここで、

y_t = x_t + v_t

d _t= h_t \bigotimes v_t

となっています。（※\bigotimesは畳み込みを表す）

さて、モデルがなんとなくわかったところで、まずは答えとなる状態と観測値を作ります。

x_t = \phi x_{t-1} + w_t

y_t = x_{t} + v_t

状態は一つ前の状態とノイズw、観測値は状態とノイズvに依存していますね。

この逆変換（ウィナー平滑化）はこんな感じになります。

d_t = \frac{(\phi^{-1} - \beta)(\phi - \beta)}{1-\beta^2} \sum^{\infty}_{k=-\infty} \beta^{|k|}y_{t+k}

\beta = \frac{( \frac{1}{r\phi} + \phi^{-1} + \phi) - \sqrt{( \frac{1}{r\phi} + \phi^{-1} + \phi)^2 -4}}{2}

\gamma = V/W



Σ(ﾟДﾟ)



もはや数学っすね。詳しくはよくわかんないですが、スペクトル変換をして周波数成分に一回落としてからもう一度足し込むみたいです。←適当

これをRで書くとこんな感じになるらしいです。

gist8e32abba01868303601d6ba7cd17c89f

スッキリしてますねー。

こんな感じで観測値から状態を一括推定できました。

感想

難しいところを思い切りすっ飛ばしたのですが、それでも難しいです。 カルマンフィルタに行き着く前に力尽きました。。。