協調フィルタリングとMatrix Factorizationについてこっそり勉強する

あんまり大きな声では言えませんが、協調フィルタリングって実はあんまり理解してないんですよね… Matrix Factorizationなんて、全くわかっていませんし。

これを言うと、いろんな人にシバかれそうなので、今回はこの2つについてこっそり勉強していこうと思います…

古典的推薦アプローチ
協調フィルタリング is 何?
- まずはイメージで考える
- 数式で考える
Matrix Factorization is 何?
- 協調フィルタリングの問題点
- 行列分解による計算量削減
参考文献
感想

古典的推薦アプローチ

古典的とは言っても、十分妥当な推薦をしてくれる技術ですし、何なら今現在でも多くのサービスで動いています。

協調フィルタリング is 何?

まずはイメージで考える

(結構ざっくりした自分の解釈としては) 協調フィルタリングの根っこの考え方は、

同じアイテムに対して似たような評価をするユーザーは、似たようなアイテムを好む

というように考えられます。

例として、amazonのようなECサイトで、トップページに表示する商品に何を表示するかを考えることとします。さて、ECサイトなので、ユーザーもたくさんいますし、販売している商品もたくさんあるはずです。すでに既存のユーザーは商品を購入しているとすると、ユーザーと商品の関係は下記のように整理されます。

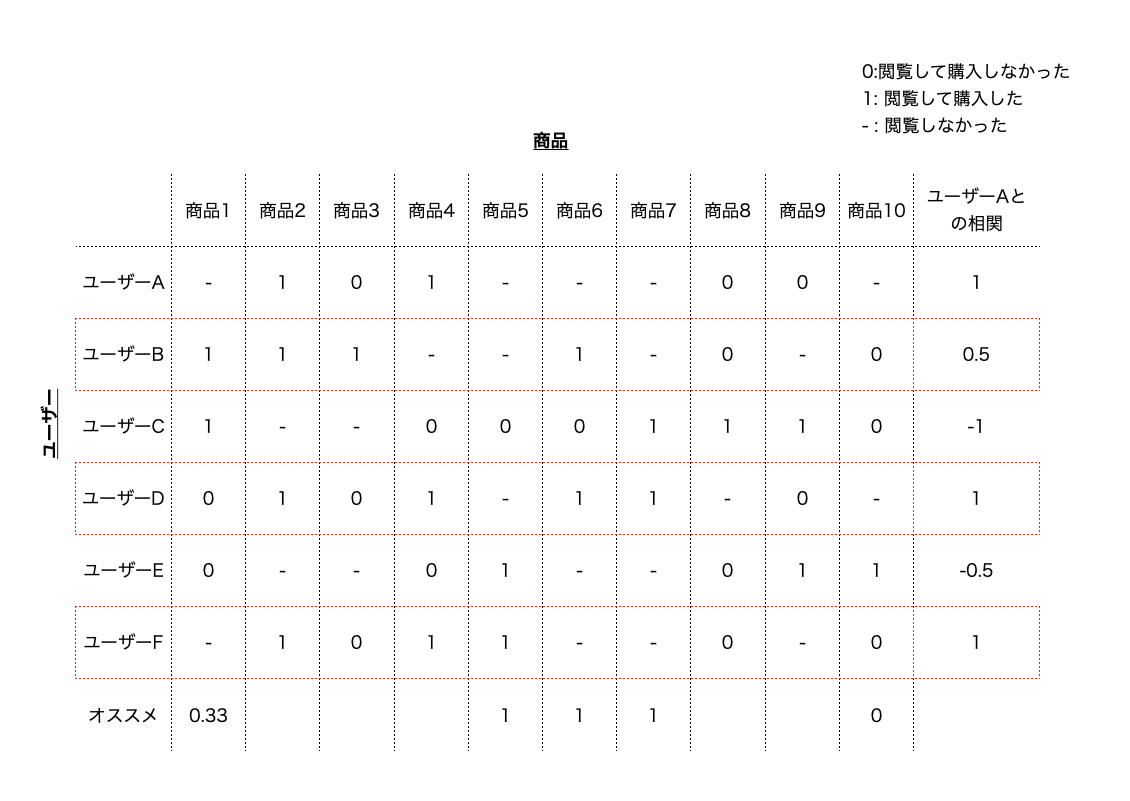
いまユーザーAに対して何の商品をトップページでおすすめしたら良いかを考えたときに、ユーザーAと同じ商品を購入しているユーザーがちらほらいることがわかるかと思います。（図中、右端の列）

今、同じアイテムに対して似たような評価をするユーザーは、似たようなアイテムを好むという仮説が正しいとすると、ユーザーAと同じ商品を購入しているユーザーが購入している商品は、ユーザーAも実は買いたいと予想できます。そこで、ユーザーAの購買履歴と似た行動をとっているユーザーを見つけます（図中赤線）これらのユーザーが購入した商品のうち、ユーザーAがまだ閲覧していない商品はおすすめしたら購入してくれそうですね。

そこで、赤線で囲ったユーザーが購入した商品に基づいて、ユーザーAにオススメすべき商品を考えてみます。すると、最下段の行のように商品のオススメ度合いが求まります。これで同じアイテムに対して似たような評価をするユーザーが比較的購入している商品が分かったので、これらの商品をおすすめしていったら良さそうです。

数式で考える

数式で考えてみます。まず、ユーザー同士がどれくらい似ているかについて考えます。ここではピアソンの相関係数を使用してユーザーの類似度を計算してみます。

$\displaystyle{ sim(i, l) = \frac{\sum_{j \in J_{il} }( y_{ij} - \bar{y_{i}}) (y_{lj} - \bar{y_{l}})} {\sqrt{\sum_{j \in J_{il} }( y_{ij} - \bar{y_{i}})^{2}} \sqrt{ \sum_{j \in J_{il} }(y_{lj} - \bar{y_{l}})^{2}}} }$

この類似度に基づいて、類似度 > x 以上の場合や類似度が高い順にn人みたいに篩いにかけることで、ユーザーiに類似したユーザーの集合 $\displaystyle{I}$ が求まります。

このままオススメアイテムについても考えてもよいのですが、場合によってはユーザーが少なくなってしまい類似度が信用できないことがあります。そのようなケースをカバーするために、重み $\displaystyle{w}$ にそのまま $\displaystyle{sim(i, l )}$ を使用せずに補正を入れることがあります。

$\displaystyle{ w(i, l) = min\{|J_{il}| / \alpha , 1\} \cdot sim(i, l) }$

ここで、 $\displaystyle{J_{il}}$ はアイテム集合で、考慮されるアイテムが多い場合には $\displaystyle{sim(i, l) }$ になるが、 $\displaystyle{J_{il}}$ が小さい( $\displaystyle{\alpha}$ より小さい)ときは重みが1より小さな重みがかかる。

さて、いま得られたユーザーiに類似したユーザーの行動をもとに、なんのアイテムがオススメなのかを考えます。

$\displaystyle{ s_{i,j} = \bar{y_{i}} + \frac{\sum_{l \in I_{j} (i)} w(i, l) (y_{lj} - \bar{y_{l}})}{ \sum_{l \in I_{j} (i)} |w(i, l)| } }$

ここで、それぞれの変数は

$s_{i,j}$ : 推定レイティング(ユーザーがどれくらいそのアイテムが好きそうか)
$y_{ij}$ : ユーザーiがアイテムjに与えるレイティング
$\bar{y_{i}}$ : ユーザーiの平均レイティング
$I_{j} (i)$ : アイテムjを評価したユーザーiに類似するユーザーの集合
$w(i, l)$ : ユーザーiがアイテムjを評価する際のユーザーlの評価に対する重み

を表しています。

言葉で数式を補足していくと、 $\displaystyle{s_{ij}}$ がユーザーiに対してアイテムjをどれくらいオススメかの度合いを表しています。右辺の第一項は、ユーザーiがアイテム全体に対して平均的にどれくらい良い反応を示すかを表しています。第二項は重み $\displaystyle{w}$ で正規化された、ユーザー全体としてアイテムjがどれくらいオススメかの度合いを表しています。

この式によって、ユーザーiに各アイテムがどれくらいのオススメ度なのかがわかるので、（すでにユーザーが購入したアイテムは除外するなど、適宜調整をした後）オススメ度が高い順に推薦してあげれば良さそうですね。一般的な協調フィルタリングはこのようにして動作しています。

Matrix Factorization is 何?

協調フィルタリングの問題点

協調フィルタリングの大きな問題点として、次元の呪いがあります。上の例ではユーザー数もアイテム数も少ない状況で考えていましたが、実際にはユーザー数・アイテム数ともに数万〜数億というオーダーになることもあります。その状況で協調フィルタリングによって推薦を行おうとすると計算量が非常に大きくなり、場合によっては計算が終わらなくなったりしてしまいます。

行列分解による計算量削減

そこで、行列分解というアプローチで計算量を削減することが考案されました。先程の推定レイティングの式について、下記のように考えます。

$\displaystyle{ s_{i,j} = \textbf{u}'_i \textbf{v}_j }$

$\displaystyle{\textbf{}{u}_i }$ , $\displaystyle{\textbf{v}_j}$ はユーザー・アイテムに関する潜在因子と呼ばれるベクトルを表しています。今、上記では1ユーザーの1アイテムについてのオススメ度合いについて見ていますが、実際には全ユーザー・全アイテムに関するオススメ度合いが欲しくなります。そのため、これを下記のように表現し直します。

$\displaystyle{ \textbf{Y}_{ij} = \textbf{U} \textbf{V'} }$

この式がもし使用できるのれあれば、我々が見つけなければ行けないのは $\displaystyle{\textbf{U}, \textbf{V}}$ の行列であり、これらのパラメータは $\displaystyle{L×n_{user}}$ , $\displaystyle{L×n_{item}}$ となり、 $\displaystyle{n_{user}×n_{item}}$ と比べて（Lが $\displaystyle{n_{user}, n_{item}}$ より小さい限り）求めなければいけない要素数は小さくなります。

このとき、厳密に $\displaystyle{\textbf{U}, \textbf{V}}$ を求めることは難しいですが、

$\displaystyle{ (\textbf{Y}_{ij} - \textbf{U} \textbf{V'})^{2} }$

のような式が最小になるように最適化問題を解くことで、近似的にこれに近い値を計算することが可能になります。これを交互最小二乗法（ALS）や確率的勾配降下法（SGD）などを使用して実際の $\displaystyle{\textbf{U}, \textbf{V}}$ の近似値を求めることで、近似的に協調フィルタリングを行うのがMatrix Factrizationということでした。