教師なし分類の代表的な手法として、k-meansがあります。 k-meansは分類自体は自動で出来るんですが、その際のクラス数はマニュアルで設定する必要があります。 そのため、どう分類されるかはここで指定するクラス数に強く依存するわけです。
この辺は人間の勘でやるのも構いませんが、この辺りまで自動でなんとかしたいと思うのが人の性かなと思います。(ほんとか?)
今回はk-meansのクラス数を自動で推定する手法を調べてみたのでそのメモです。
まずは調べる
ちょっと調べてみるとこんな感じの記事が見つかりました。
何やらX-meansやらG-meansなるものがあるようで、この辺を使うといい感じにクラスタ数を設定できるようです。
中の理屈については、上記の記事を御覧ください。
また、今回は取り上げませんが、scikit-learnのチートシートによればMeanShiftとVBGMMが紹介されています。
クラスタ数を自動で設定するクラスタリングにも、色々手法があるということはわかりました。
やってみる
今回はX-meansやらG-meansの使い方を見ていきたいと思います。
これら2つは、PyClusteringのライブラリで利用することができます。
この辺を使って、クラスタ数を自動で設定するクラスタリングをやってみたいと思います。
下準備として、16次元の特徴量を持った 8クラスのデータを生成しておきます。 それを PCAで次元圧縮して分布を確認してみるとこんな感じでした。
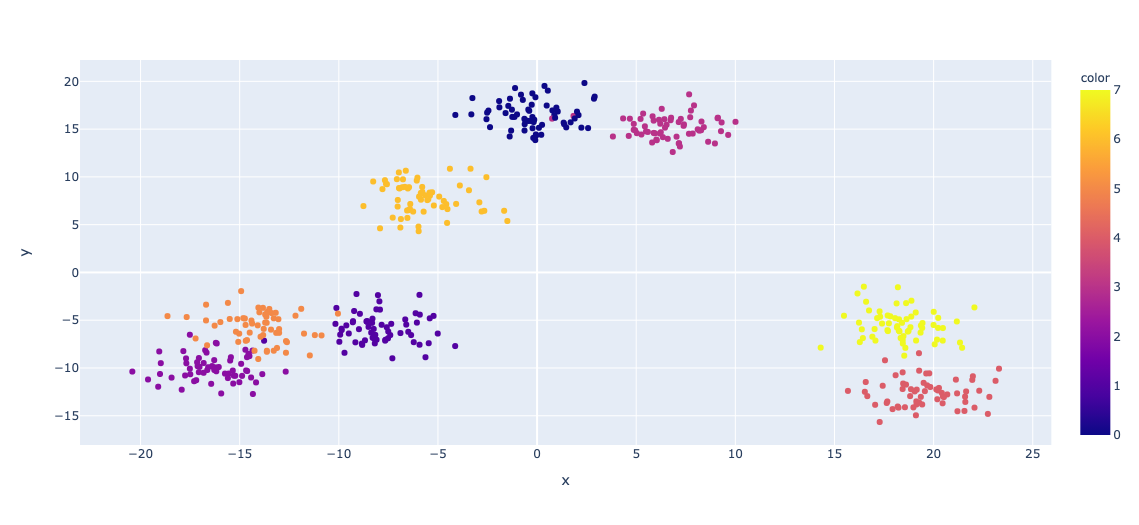
普通のk-means
まずは普通にk-meansをやるとどうなるかをやってみます。
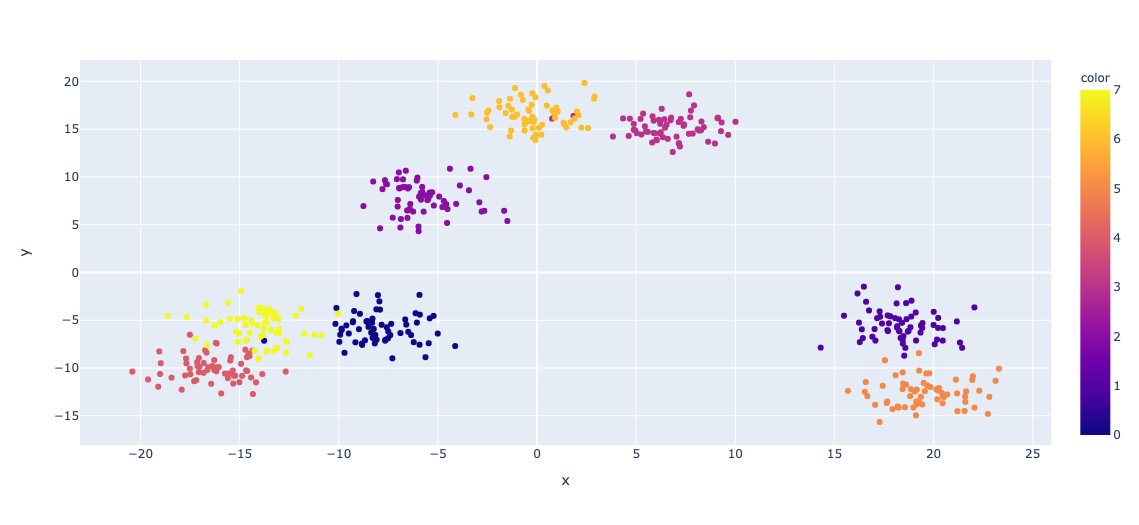
元データと全く同じラベルに分類されていることがわかります。 本当はここまでうまくいくことはあまりないんですが、今回は元のデータがわかりやすかったんでしょう。
X-means
前提条件は終わったので、本題のX-meansをサクッとやってみます。
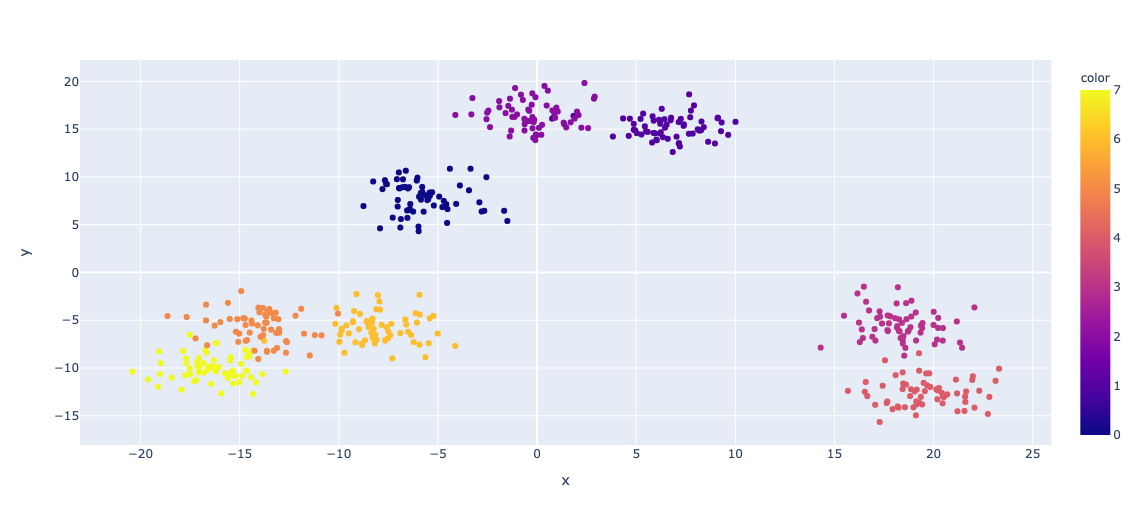
こちらはクラス数を指定していませんが、自動で0~7の8クラスに分類されていることがわかります。 いい感じですね。
G-means
今度はG-meansです。
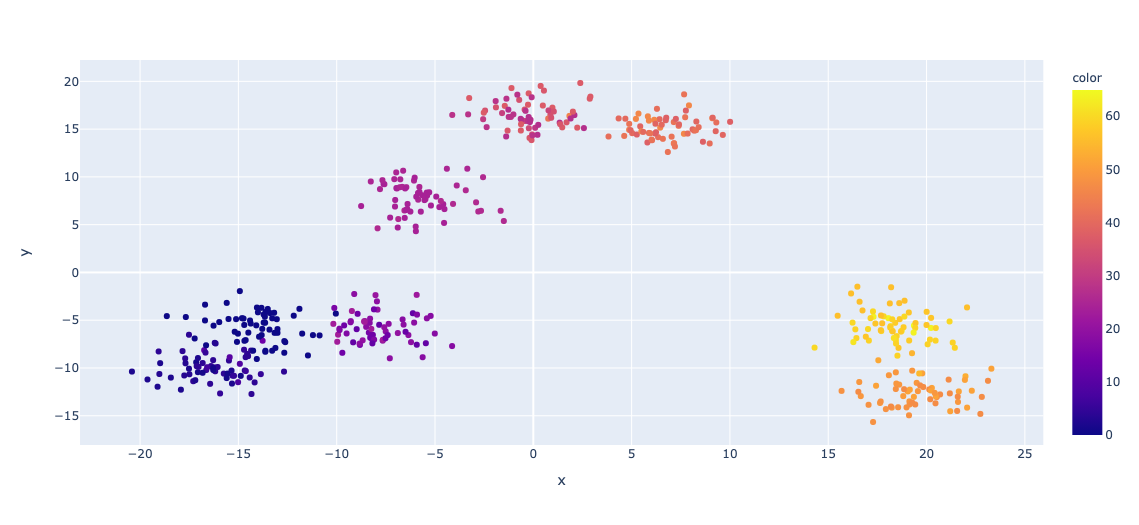
色だけ見るとうまく分類されていそうなんですが、カラースケールを見ると値がかなり大きくなってしまっていることがわかります。 実際のクラス数を見ると 0〜65の66クラスに分類されてしまっていました。 元データとしては同じクラスに属しているはずのデータが細かく分類されてしまった形になっています。 参考にさせていただいた記事では普通にうまくいっていたので、次元数とかが影響しているんでしょう。
実際に使うときには、確認しながら使っていかないといけないかもしれませんね。
使ったコード
一応使ったコードはこちらになります。
参考文献
この記事を書くにあたって下記の記事を参考にさせていただきました。
感想
ちょっと別のことをやっていて、k-meansのクラス数を自動で決定させたかったので調べてみた次第です。
エルボー図やシルエット図を用いた手法だと、ある程度理論に基づいてクラス数を推定出来るものの、一部人間の主観が介在してしまったりしまいます。 今回の方法ならば、人間の主観を排除してクラス数を推定できる点では便利だと思いました。(主観が入ると場合によっては変なイチャモンをつけられたりするので)
これまでやってこなかったようなことなので、非常に勉強になりました。