基本的な推薦アルゴリズムを書いて眺める

この記事は（1人で）基礎から学ぶ推薦システム Advent Calendar 2022の11日目の記事です。

推薦関係のアルゴリズムは現在でも新しいアルゴリズムがありますが、古典的なアルゴリズムとして協調フィルタリング〜Factorization Machineが挙げられると思います。今回はこれらのクラシカル（？）な推薦アルゴリズムを書いて眺めてみたいと思います。

モデル
実装
評価
サンプルコード
参考文献
感想

モデル

協調フィルタリング

協調フィルタリングと一口に言っても色々あって、協調フィルタリングとは？基本的な考え方や種類を解説によれば下記のように分類できるそうです。

メモリベース : トランザクションデータを基にしてレコメンデーションを行う協調フィルタリング
- ユーザーベース
- アイテムベース
モデルベース : ユーザーによる商品の評価データを抽象化して活用
ハイブリッド : 協調フィルタリングとコンテンツベースフィルタリングの組み合わせ

今回はユーザーベースの協調フィルタリングについてやってみようと思います。イメージとしては、ユーザー・アイテムの行列が下記のような行列で表現されている状態を考えます。

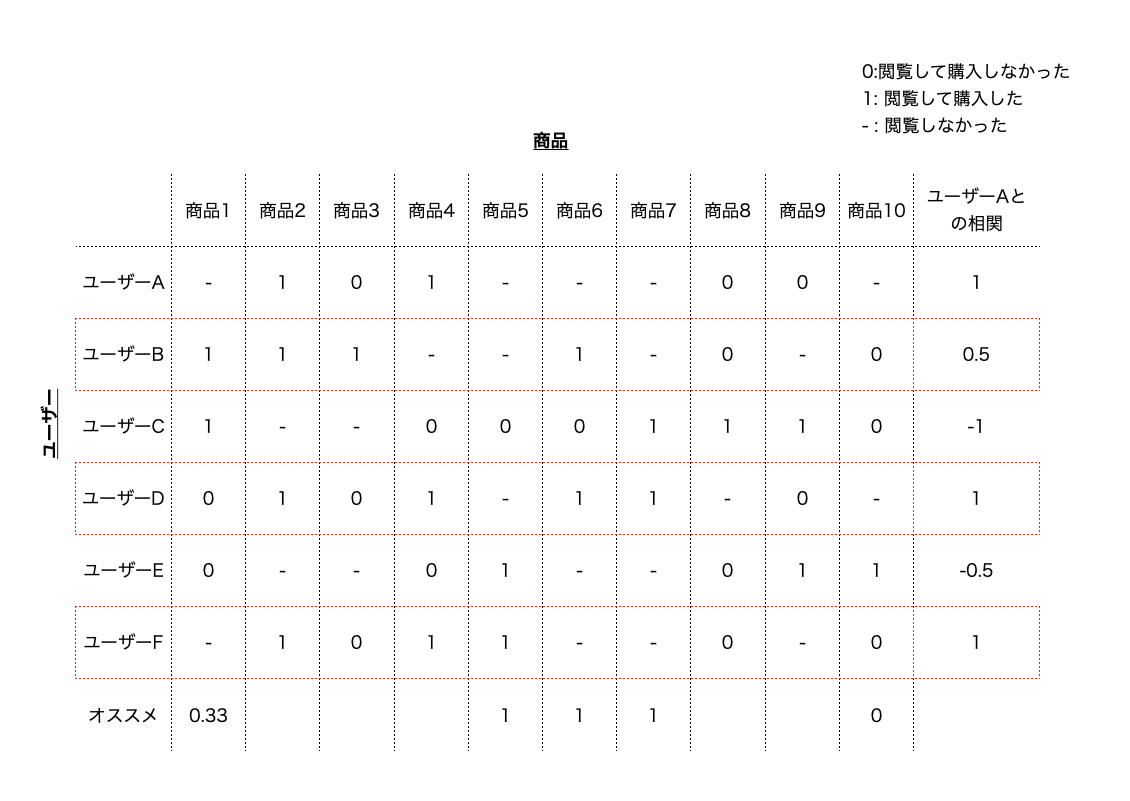
このような状態を考えたときに、ユーザーベースの協調フィルタリングでは大まかに下記の手順で計算を行います。

ユーザー同士の類似度を計算
似た傾向を持つユーザーを選別
類似度と別のユーザーの評価値から未評価のアイテムの評価値の推定値を計算

1. ユーザー同士の類似度

ユーザー同士の類似度にはピアソンの相関係数を使用してユーザーの類似度を計算してみます。式としては下記のように計算されます。

$\displaystyle{ sim(i, l) = \frac{\sum_{j \in J_{il} }( y_{ij} - \bar{y_{i}}) (y_{lj} - \bar{y_{l}})} {\sqrt{\sum_{j \in J_{il} }( y_{ij} - \bar{y_{i}})^{2}} \sqrt{ \sum_{j \in J_{il} }(y_{lj} - \bar{y_{l}})^{2}}} }$

このユーザーi, jの類似度は、値が大きいほど類似していると考えることができます。

2. 似た傾向を持つユーザーを選別

このままオススメアイテムについても考えてもよいのですが、あまり類似度が低いユーザーの嗜好は参考にならないかもしれません。そのようなケースをカバーするために、重み $\displaystyle{w}$ にそのまま $\displaystyle{sim(i, l )}$ を使用せずに補正を入れることがあります。

上で計算したユーザー同士の類似度に基づいて、類似度 > x 以上の場合や類似度が高い順にn人みたいに篩いにかけることで、ユーザーiに類似したユーザーの集合 $\displaystyle{I}$ が求まります。

3. 類似度と別のユーザーの評価値から未評価のアイテムの評価値の推定値を計算

さて、いま得られたユーザーiに類似したユーザーの行動をもとに、なんのアイテムがオススメなのかを考えます。

$\displaystyle{ s_{i,j} = \bar{y_{i}} + \frac{\sum_{l \in I_{j} (i)} w(i, l) (y_{lj} - \bar{y_{l}})}{ \sum_{l \in I_{j} (i)} |w(i, l)| } }$

ここで、それぞれの変数は

$s_{i,j}$ : 推定レイティング(ユーザーがどれくらいそのアイテムが好きそうか)
$y_{ij}$ : ユーザーiがアイテムjに与えるレイティング
$\bar{y_{i}}$ : ユーザーiの平均レイティング
$I_{j} (i)$ : アイテムjを評価したユーザーiに類似するユーザーの集合
$w(i, l)$ : ユーザーiがアイテムjを評価する際のユーザーlの評価に対する重み

を表しています。

この式によって、ユーザーiに各アイテムがどれくらいのオススメ度なのかがわかるので、（すでにユーザーが購入したアイテムは除外するなど、適宜調整をした後）オススメ度が高い順に推薦してあげれば良さそうですね。実際にはもっと細かいところはありますが、だいたいこのような計算によって動作しています。

Matrix Factorization

協調フィルタリングはあまり計算効率が良くないので、ユーザー・アイテムが大規模になるときには実行時間が長時間化したり、場合によって実行自体が終わらなくなってしまう問題があります。

こうした問題を解決するために、計算量をコンパクトにしたMatrix Factorizationという手法が使われることがあります Matrix Factorizationは、大体下記のような流れで計算することができます。

ユーザー・アイテムに関する潜在変数を設定
潜在変数を使用してユーザー-アイテムの評価値を推定
誤差関数に従って潜在変数を修正

潜在変数を仮定して実測値との差分から最適化を行っていきます。イメージとしては、2つの行列の積を計算して、すでに評価済みの要素について実際の値と積の結果が近づくようにはじめの2つの行列の要素を探索していくイメージです。

Factorization Machine

因数分解マシン(Factorization Machine, FM)は、任意の実数値で表現された特徴量を低次元の潜在因子空間に写像する汎用的な教師付き学習モデルです。

Matrix Factorizationではあくまで行列の掛け算で協調フィルタリングを表現したものになってましたが、Factorization MachineではUser、Itemの系列データをすべて横持ちの学習データとして保持し、1行ごとにインタラクションを表現します。

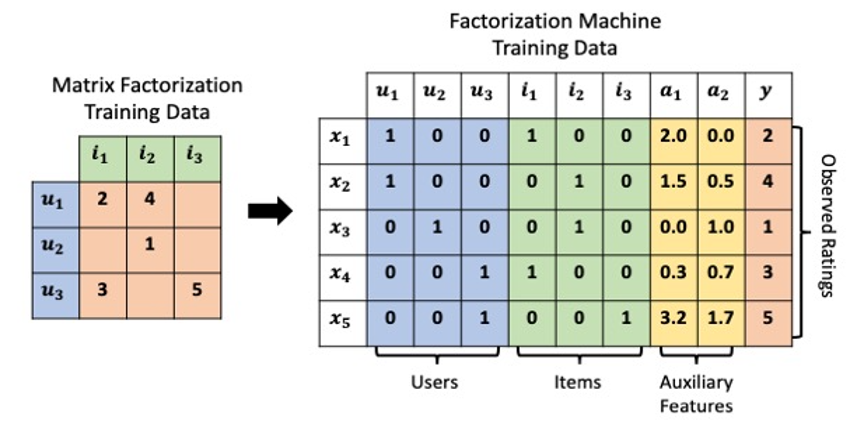
(Factorization Machines for Item Recommendation with Implicit Feedback Data | by Eric Lundquist | Towards Data Science より引用)

この状況で、下記の式のように計算します。

$\displaystyle{ f(x) = w_{0} + \sum^{P}_{p=1} w_p x_p + \sum^{P-1}_{p=1} \sum^{P}_{q=p-1} \langle v_{p}, v_{q} \rangle x_p x_q }$

ここで、 $\displaystyle{\langle v_{p}, v_{p} \rangle}$ は潜在ベクトルの内積を表します。

この式ですが、右辺第3項に関して

$\displaystyle{ \hat{\textbf{y}}(X) = \frac{1}{2} ( square(XV) - (square(X) \times square(V) )).sum(rowwise), }$

のように変形することができ、行列積の組み合わせで効率よく計算できます。理論はやや数式ばっていますが、実際に書いてみると単純なニューラルネットで記述することができるようになります。

実装

実装の詳細はgithubに上げておくのそっちを見てもらうとして、アルゴリズムのコアになる部分だけここではピックアップしようと思います。

協調フィルタリング

めんどくさい計算とかをすっ飛ばすと、計算しているのはこんな流れになるかと思います。

    def run(self):
        """協調フィルタリングの計算

        Returns:
            _type_: _description_
        """

        df = self.df

        sim = self.pearson_coefficient(df)
        avg_user_rating = self.average_user_rating(df)
        y_ybar = self.user_rating_diff(df, avg_user_rating)

        d = self.sum_sim(sim, df)
        c = sim.fillna(0).dot(y_ybar.fillna(0))

        return avg_user_rating.add((c/d))

あとは、内部に実装してある関数の中身を実装するだけで普通に実装できます。

Matrix Factorization

MFに関しては、下記のような実装がわかりやすかったです。

class MF():
    def __init__(self, R, K, alpha, beta, iterations):
        """
        Perform matrix factorization to predict empty
        entries in a matrix.

        Arguments
        - R (ndarray)   : user-item rating matrix
        - K (int)       : number of latent dimensions
        - alpha (float) : learning rate
        - beta (float)  : regularization parameter
        """

        self.R = R
        self.num_users, self.num_items = R.shape
        self.K = K
        self.alpha = alpha
        self.beta = beta
        self.iterations = iterations

    def train(self):
        # user latent feature matrix
        self.P = np.random.normal(scale=1./self.K, size=(self.num_users, self.K))
        # item latent feature matrix
        self.Q = np.random.normal(scale=1./self.K, size=(self.num_items, self.K))

        # Initialize the biases
        self.b_u = np.zeros(self.num_users)
        self.b_i = np.zeros(self.num_items)
        self.b = np.mean(self.R[np.where(self.R != 0)])

        # Create a list of training samples
        self.samples = [
            (i, j, self.R[i, j])
            for i in range(self.num_users)
            for j in range(self.num_items)
            if self.R[i, j] > 0
        ]

        # Perform stochastic gradient descent for number of iterations
        training_process = []
        for i in range(self.iterations):
            np.random.shuffle(self.samples)
            self.sgd()
            rmse = self.rmse()
            training_process.append((i, rmse))
            if (i+1) % 10 == 0:
                print("Iteration: %d ; error = %.4f" % (i+1, rmse))

        return training_process


    def rmse(self):
        """
        total root mean square error
        """
        xs, ys = self.R.nonzero() # 欠損値は計算対象から外れている
        predicted = self.full_matrix()
        error = 0
        for x, y in zip(xs, ys):
            error += pow(self.R[x, y] - predicted[x, y], 2)
        return np.sqrt(error / len(xs))

    def sgd(self):
        """
        Perform stochastic graident descent
        """
        for i, j, r in self.samples:
            # Computer prediction and error
            prediction = self.get_rating(i, j)
            e = (r - prediction)

            # Update biases
            self.b_u[i] += self.alpha * (e - self.beta * self.b_u[i])
            self.b_i[j] += self.alpha * (e - self.beta * self.b_i[j])

            # Update user and item latent feature matrices
            self.P[i, :] += self.alpha * (e * self.Q[j, :] - self.beta * self.P[i,:])
            self.Q[j, :] += self.alpha * (e * self.P[i, :] - self.beta * self.Q[j,:])

    def get_rating(self, i, j):
        """
        Get the predicted rating of user i and item j
        """
        prediction = self.b + self.b_u[i] + self.b_i[j] + self.P[i, :].dot(self.Q[j, :].T)
        return prediction

    def full_matrix(self):
        """
        Computer the full matrix using the resultant biases, P and Q
        """
        return self.b + self.b_u[:,np.newaxis] + self.b_i[np.newaxis:,] + self.P.dot(self.Q.T)

PとQが潜在変数を含んだ行列になっていて、それらを学習していく実装になっていますね。

Factorization Machine

この辺からライブラリを使用したくなったのでPyTorch（PyTorch Lightning）を使用して実装しています。ただ、根幹の数式はforwardに記述された内容がすべてなのでロジック自体はスッキリしていることがわかります。（学習のコードを書くのがめんどくさいだけ）

class FM(pl.LightningModule):
    """ Factorization Machine """

    def __init__(self,
                 n: int = None,
                 k: int = None):
        """
        Args:
            n (int, optional): weight matrixのサイズ
            k (int, optional): 学習データの行数
        """
        super().__init__()
        # Initially we fill V with random values sampled from Gaussian distribution
        # NB: use nn.Parameter to compute gradients
        self.V = nn.Parameter(torch.randn(n, k), requires_grad=True)
        self.lin = nn.Linear(n, 1)

        # Loss
        self.loss_fn = nn.MSELoss()

        # コンソールログ出力用の変数
        self.log_outputs = {}

    def forward(self, x):
        out_1 = torch.matmul(x, self.V).pow(2).sum(1, keepdim=True)  # S_1^2
        out_2 = torch.matmul(x.pow(2), self.V.pow(2)).sum(
            1, keepdim=True)  # S_2
        out_inter = 0.5*(out_1 - out_2)
        out_lin = self.lin(x)
        out = out_inter + out_lin

        return out

    def configure_optimizers(self):
        optimizer = torch.optim.Adam(
            self.parameters(), lr=0.02)
        return optimizer

    # 学習のstep内の処理
    def training_step(self, batch, batch_index):
        X, y = batch
        pred = self(X)
        loss = self.loss_fn(pred, y)
        return {'loss': loss}

    # validのstep内の処理
    def validation_step(self, batch, batch_index):
        X, y = batch
        pred = self(X)
        loss = self.loss_fn(pred, y)
        return {'val_loss': loss}

    # 学習の全バッチ終了時の処理
    def training_epoch_end(self, outputs) -> None:
        train_loss = torch.stack([x['loss'] for x in outputs]).mean()
        self.log_outputs["loss"] = train_loss
        return

    # validのepoch終了時の処理、ロスの集計などを行う
    def validation_epoch_end(self, outputs) -> None:
        valid_loss = torch.stack([x['val_loss'] for x in outputs]).mean()
        self.log_dict({"valid_loss": valid_loss})
        self.log_outputs["valid_loss"] = valid_loss
        return

    # epoch開始時の処理
    def on_train_epoch_start(self) -> None:
        self.print(
            f"Epoch {self.trainer.current_epoch+1}/{self.trainer.max_epochs}")
        return super().on_train_epoch_start()

    # epoch終了時の処理
    def on_train_epoch_end(self) -> None:
        train_loss = self.log_outputs["loss"]
        valid_loss = self.log_outputs["valid_loss"]
        self.print(f"loss: {train_loss:.3f} - val_loss: {valid_loss:.3f}")
        return super().on_train_epoch_end()

    # 学習開始時の処理
    def on_train_start(self) -> None:
        self.print(f"Train start")
        return super().on_train_start()

    # 学習終了時の処理
    def on_train_end(self) -> None:
        self.print(f"Train end")
        return super().on_train_end()

評価

勉強で試しに書いてみているだけなので、モデルの精度評価にどこまでの意味があるのかは疑問ですが、一応簡単に評価ぐらいはやってみようと思います。今回試したアルゴリズムはすべてuser-itemの評価値を推定しているので、実際の評価値と推定された評価値のズレをRMSEで測定してみます。

アルゴリズム	RMSE	Recall@10	nDCG@10
ランダム	1.910	0.180	0.777
average（item毎の平均評価値を推定評価値とする）	1.031	0.221	0.876
協調フィルタリング	1.048	0.221	0.881
Matrix Factorization	1.262	0.187	0.799
Factorization Machine	52.830	0.174	0.778

一応協調フィルタリングが一番良さそうな結果にはなってそうなので良かったです。

Factorization Machineの値が悪いのは、特徴量作成をかなり簡略化しているのが原因だと思っているので、ちゃんと特徴量を作ればもっと値は良くなると思います。気が向いたら特徴量追加して直しておきます。

まあ、これらの指標が良いか悪いかは、現状ではよくわかりませんが今後いろんなアルゴリズムを試す中でわかってくるんでしょう。

サンプルコード

これに使用した実装のコードはこちらにあります。

github.com

参考文献

この記事を書くにあたって、下記の文献を参考にさせていただきました。

感想

どうでも良いですけど、コードは日々書いてないとしんどいですね。全然上手に書けませんでした。

Re:ゼロから始めるML生活

どちらかといえばエミリア派です

基本的な推薦アルゴリズムを書いて眺める

モデル

協調フィルタリング

1. ユーザー同士の類似度

2. 似た傾向を持つユーザーを選別

3. 類似度と別のユーザーの評価値から未評価のアイテムの評価値の推定値を計算

Matrix Factorization

Factorization Machine

実装

協調フィルタリング

Matrix Factorization

Factorization Machine

評価

サンプルコード

参考文献

感想