最近時系列系のデータについて扱う機会があって、その関係でちょっと勉強してました。
世の中に時系列分析の本はそこそこ出ている印象ですが、多くの場合でR言語での実装が紹介されており、Pythonでの実装が紹介されている文献はあまり多くない印象です。 ということで、数少ないPythonでの時系列分析を取り扱ったこちらの書籍を読んでみました。

時系列解析: 自己回帰型モデル・状態空間モデル・異常検知 (Advanced Python)
- 作者:直希, 島田
- 発売日: 2019/09/07
- メディア: 単行本
今回はこちらの書籍で、時系列分析について復習してみたのでそのメモです。
時系列分析でとりあえず考えること
この辺はその道の書籍を読んでいただければ、ちゃんと理屈が書いてあると思うので、適当に自分の頭の整理のために書いていきたいと思います。
そもそも時系列データとは
久しぶりなんで、基本的な定義についても確認したいと思います。
時系列データは,測定対象の,ある側面をある時間間隔で観測した結果の集まりである.具体例として毎日の気温や降水量,営業日ごとの株価の終値があげられる. 時系列解析: 自己回帰型モデル・状態空間モデル・異常検知
とあります。ポイントとなる考えとしては、一定の時間間隔で取得したデータであるという前提があります。 単純に取得したデータを時刻ごとに並べたものではなく、一定の間隔で取得していることを前提に取り扱う必要があります。
時系列データで考えること
そんな時系列データですが、これをモデリングする上で最低限考えるべき要素について確認していきます。
データにノイズが乗っている
まず、得られているデータには、従うであろう理想的なモデルに対してノイズが加わっていることを考えないといけません。 理想的な環境下で取得されたデータ出ない限り、必ずと言ってよいほどノイズは乗ってきます。 そのノイズまでモデリングの対象にしてしまうと、データが従うモデルを捉えることが難しくなります。
ノイズの除去の方法としては、時系列データの移動平均を取ることなどが考えれます。 移動平均を取ることによって、ノイズの影響を小さくするような効果が期待できます。 ただし、移動平均のウィンドウサイズについては検討が必要で、ウィンドウサイズが大きいとノイズの影響は小さくなると考えられますが大きい範囲でのデータの傾向を見ていくことになり、逆にウィンドウサイズが小さいときにはノイズの影響が残りやすくなります。 その点を考慮した状態で考える必要があります。
時間方向の傾向がある
時系列データの特徴として、時間方向に一定の傾向があることがあります。
時間方向の傾向としては、trendとseasonality、そして、これらを除いたときに得られるresidualがあります。 trendは時刻が進むにつれて、観測値がどのような傾向にあるかといった大きな範囲の傾向を表します。 seasonalityは、特定の周期で観測値が大きくなったり小さくなったりする傾向を表します。

この傾向が確認できる際には、これはモデリングの際に有用な情報となります。
試しにこちらの記事をなぞって確認してみます。
とりあえず、確認してみたいと思います。
trendとseasonality、residualはこのようにして分解して確認することができました。
自己相関がある
最後に、自分自身の値に相関関係があることを考えます。 もう少し具体的に考えると、時刻tの状態が時刻t-1の値に影響を受けている可能性があるということを考慮する必要があります。
これはコレログラムというもので確認することができます。
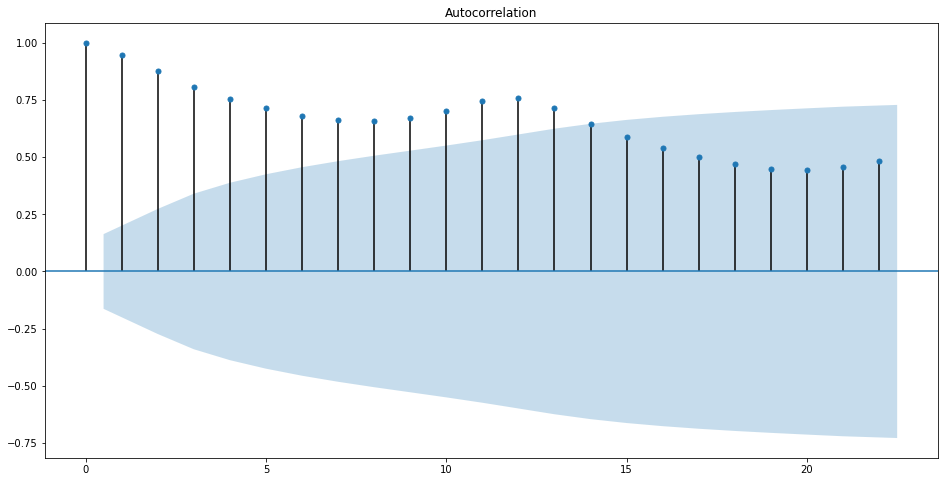
読み方としては、ある時点からずらした量(ラグ)を横軸にとり、計算した相関係数を縦軸にとっています。 したがって、上下にむかって相関係数が大きいところは、その周波数で周期性があると考えられます。
こっちも実際に確認してみます。
上2つは、系列データをそのまま分析した結果、下2つはtrendだけを抽出して分析した結果となっています。 下2つに関しては、トレンドについての結果なので、直前の値に大きく影響を受けていることを表しており、きちんとトレンドを抽出できているようです。
カルマンフィルタ
ここまでが、時系列データについてモデリングする前にデータから最低限確認したいことだと思ってます。 ここから、実際のモデリングを考えていきます。
今回は都合上、ARIMAなどの自己相関モデルについては割愛します。 自己相関モデルについて知りたい方は下記の記事などを参考にやったらできると思います。
今回は状態空間モデルを対象にやっていきたいと思います。 状態空間モデルとは、ざっくりいうと目に見える観測値の他に、観測できない状態を仮定されているモデルです。
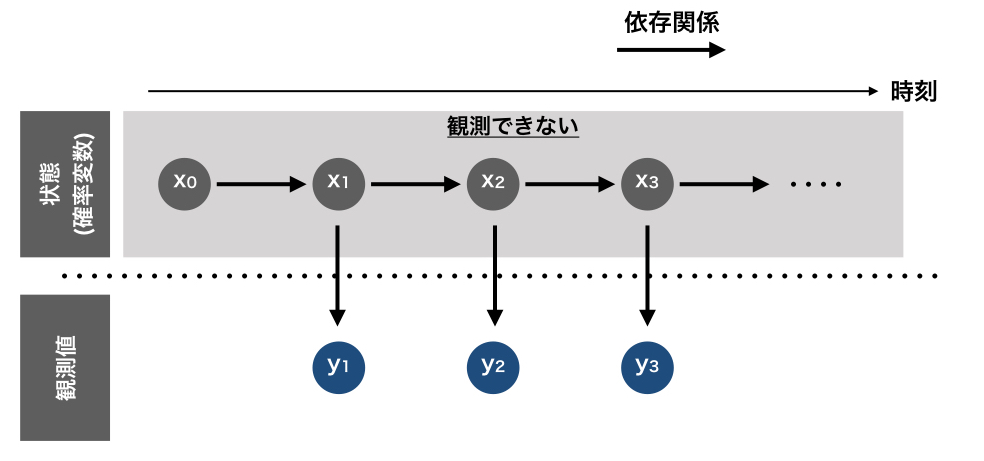
状態と観測値は、それぞれ状態方程式と観測方程式で振る舞いが表現され、状態は直前の状態から決定され、観測値は状態によって決定されるものと仮定されています。
(状態方程式、システム方程式)
(観測方程式)
この状態空間モデルについて、まずはカルマンフィルタを使って解いてみたいと思います。
カルマンフィルタは、「状態の1期先予測」と「観測値を用いた状態の補正」を交互に繰り返すことで、モデルのパラメータを推定していく手法です。 細かい話はこちらの書籍にわかりやすく記載されているのでこちらをご参照ください。
カルマンフィルタでは、下記のような条件が想定されています。
- 状態の変化が線形
- ノイズが正規分布に従う
このような条件を満たす場合にはカルマンフィルタを使用することで効率よく状態を推定することができます。
予測・フィルタリング・平滑化
状態は実際に観測することができないということは上で述べました。 ということで、観測値から状態を推定するということが必要になってきます。
時系列データでは、各時点のデータが与えられますが、データにはそれぞれ鮮度があります。 そして、どの時点のデータを使用して状態を推定するかによって、推定された状態の信頼性は異なりますし、その推定方法の名称も予測・フィルタリング・平滑化と変わっています。 それぞれの違いとしては、より新しい観測値を使用して推定したほうが信頼性が高そうというような違いがあり、これは直感に反さないかと思います。
予測とは、下図のように過去の観測値を使って未来の状態を推定する計算を指します。
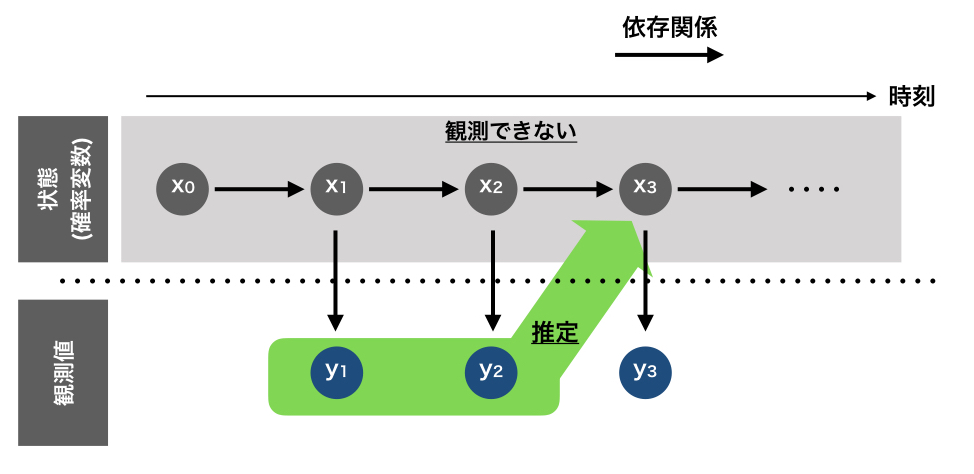
予測は、あくまで予測なので実際の値とは異なることが大いに考えられます。 そこで、現在の値を使用して予測の値を補正するといったことが行われます。 フィルタリングは下図のように、手に入った観測値を使って状態を推定することを指します。
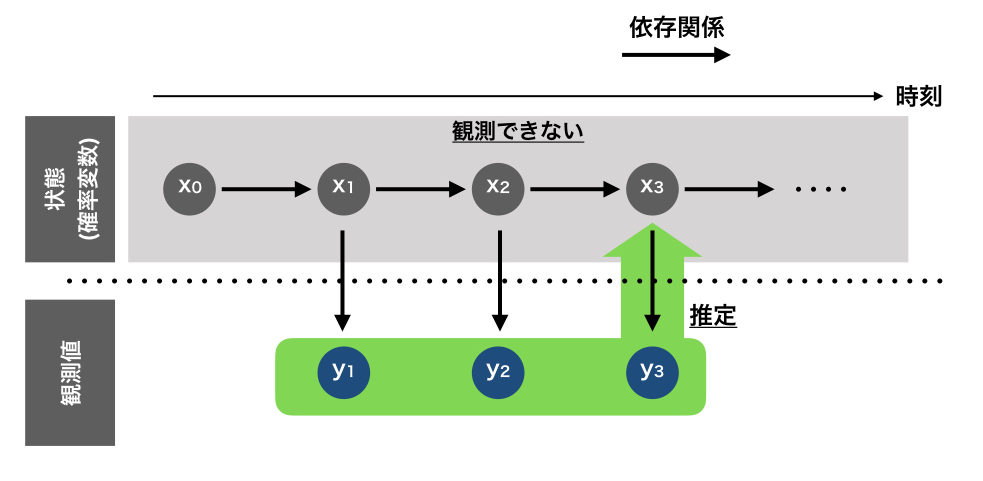
平滑化とは、未来の観測値を使って過去の状態を補正する計算を指します。
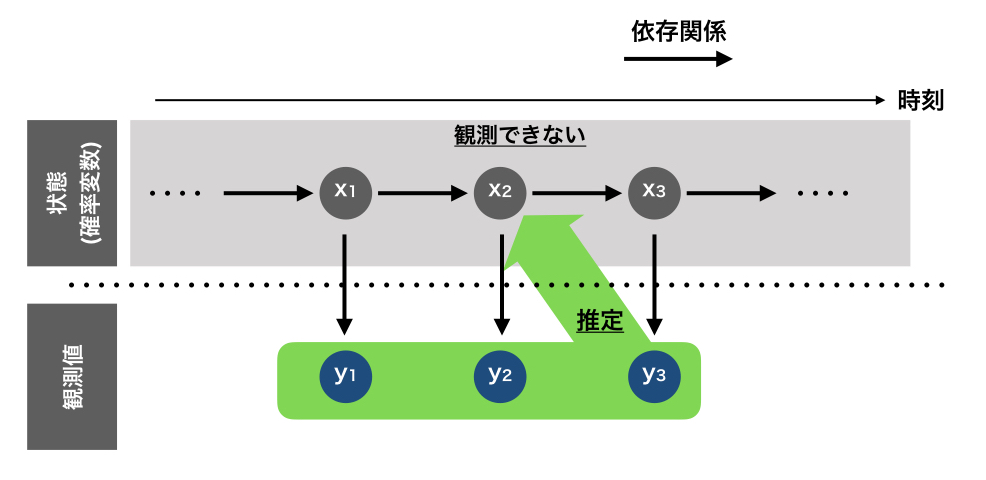
平滑化を使用すると、ノイズの影響を更に軽減するということに繋がります。 ただし、最新の観測値の状態についての精度という意味では、フィルタリングと平滑化の結果は一致するため、あくまでノイズを除去して知識発見という意味合いが強い場面で使用されます。
難しい理屈の話は参考にした書籍に譲るとして、実際にカルマンフィルタを使って時系列データをモデリングしてみたいと思います。
ざっくりとした仕組みの理解
状態空間モデルといっても、その中に細かくモデルがあり、状態方程式が異なります。 カルマンフィルタで行う「状態の1期先予測」は、個別のモデルの状態方程式に従って状態を予測します。
一方、「観測値を用いた状態の補正」については、カルマンゲインという量を使用して、下記の式のように補正がおこなわれます。
補正後の状態=補正前の状態+カルマンゲイン*(実際の値-予測された観測値)
カルマンゲインは、状態の予測誤差と観測誤差の分散に応じて決定され、1以下の数値を取ります。 そのため、状態の予測誤差・観測誤差の分散によって、信用できる範囲で状態を補正していくということを行っています。
この予測と補正を繰り返して更に未来まで予測していくのがカルマンフィルタになります。
Pythonのコードサンプル
さて、難しい話はこの辺にして、詳しい話は参考にした文献をご参照ください。 実際の実装を確認します。 コード自体は付録にあるので、そちらをご参照ください。
やってみると、学習用のデータの部分についてはフィッティングできていることが確認できます。 一方、テスト用の未来のデータの予測に関しては、あまり正解していないように見受けられます。
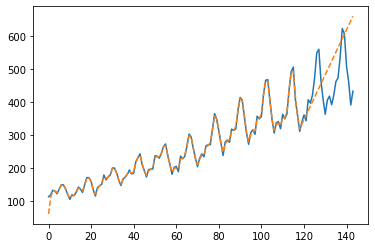
この予測と実測のズレを修正していくことに関しては、参考書籍をご確認ください。 (季節調整モデルにしたり、EMアルゴリズムでパラメータを推定したり、いろいろやってます。)
MCMC
カルマンフィルタは線形ガウス型モデルの事象が仮定されており、状態の変化が非線形の場合やノイズがガウス型でない場合などには適しません。 そこで、これらに対して何らかの近似を置くことでこの問題に対応していくことになり、その一つの手法がMCMC(マルコフ連鎖モンテカルロ法)と呼ばれるものです。
MCMCは、確率分布が与えられたときに、その確率分布に従う標本を作る手法です。 そして、状態空間モデルの文脈においては、状態に関する確率密度関数が与えられた際に、それを積分計算で解くのではなく、確率分布に従う標本をもとにモンテカルロ法を用いて解くということになります。
このあたりについては、実は過去にブログを書いていたらしいので、そちらもご参照ください。(機会があったらMCMC自体の理論もちゃんと復習します)
さて、このあたりのベイズ関係の実装をする際には、R言語が使用されることが比較的多い印象ですが、Pythonでも実装は可能になっています。 ライブラリとしては、ざっと調べたところPyStanやPyMCがよく使用されているようでした。
pymc3での実装に関しては、pymcの使い方がいまいち理解しきれていないので、わかったらそのうち書くようにします。
粒子フィルタ
逐次解法であるカルマンフィルタに対して、MCMCは一括解法という区分になり、計算効率が非常に悪いことが知られています。 固定された時系列のモデリングに対しては十分かと思われますが、徐々に系列データが増えていく環境下で使用する場合には、計算効率の点で使いにくくなることが考えられます。
粒子フィルタは、非線形非ガウス型のモデルにおいて逐次解法で解くことができるアルゴリズムです。
粒子フィルタのイメージはこちらの記事がわかりやすかったです。
状態は必ずしもガウス型の関数になっているとは限らず、そうでない場合においては何らかの近似が求められます。 そこで、状態の確率分布を粒子近似(確率密度が高いところに粒子が密集するように分布を表現)を使用します。
この手法によって、下記のような流れで計算を行うことで状態を推定していきます。
- 時刻tの時点での粒子の分布から、1期先予測
- 時刻t+1の時点での観測値を使用してフィルタ分布を求め、各粒子に対して重要度に応じて重み付けを行う
- 重み付けされた粒子の分布からリサンプリングして、それを時刻t+1での状態の分布とする
- 1から3を繰り返す
Pythonのコードサンプル
カルマンフィルタ同様、参考書籍にコードサンプルがあるので、そちらをそのまま拝借してやってみます。
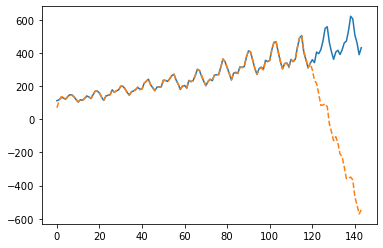
こちらもカルマンフィルタと同様に、学習用のデータの部分についてはフィッティングできていることが確認できます。 一方、テストデータの範囲では、実績と予測線がかなり乖離していることがわかります。 こちらも、参考図書では予測と実績に関して補正が行われていきます。
参考文献
時系列分析の主な手法について勉強する際には、R言語での紹介になりますが、下記の書籍がわかりやすく解説されています。

時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装
- 作者:真哉, 馬場
- 発売日: 2018/02/14
- メディア: 単行本
また、解説は若干難しいですが、こちらの書籍も詳しく解説されているので、理論について学ぶ際には良いと思います。
Pythonで時系列分析を行うことに関しては、今回主に参考にした、こちらの書籍が本記事執筆時点では一番詳しく書いてある気がします。

時系列解析: 自己回帰型モデル・状態空間モデル・異常検知 (Advanced Python)
- 作者:直希, 島田
- 発売日: 2019/09/07
- メディア: 単行本
その他、自分が過去に書いた残骸はこの辺に転がっています。
感想
ちょっと時系列分析の復習をする機会があったので、その延長で記事を書いてみました。
実装の部分はサンプルコードを眺めただけですが、予測のズレに関しては修正方法まで後で見てみたいと思います。 MCMCに関しては、覚えてたらそのうち実装を追記するかもしれないです。。。(すいません)
久しぶりに時系列分析をやってみると、意外と覚えてなかったのと、改めて勉強してみると前回勉強したときよりは理解が進んだ気がします。 良い勉強になりました。
