EMアルゴリズムについてのメモ - Re:ゼロから始めるML生活

最近この辺りの本を読んでいるんですが、その中にEMアルゴリズムというものが登場します。

推薦システム: 統計的機械学習の理論と実践

作者:Deepak K. Agarwal,Bee‐Chung Chen
出版社/メーカー: 共立出版
発売日: 2018/04/21
メディア: 単行本

トピックモデル (機械学習プロフェッショナルシリーズ)

作者:岩田具治
出版社/メーカー: 講談社
発売日: 2015/04/08
メディア: 単行本（ソフトカバー）

実は過去にも登場しているんですが、そのときはよくわからないままさらっと流していました。

www.nogawanogawa.com

機械学習ド素人なんで、はっきり言ってよくわかりませんでした。こういうときは、もっと初学者向けの本を読むとわかることがあるので、今回はEMアルゴリズムの勉強のためだけにこちらの本を読んでみました。

しくみがわかるベイズ統計と機械学習

作者:手塚太郎
出版社/メーカー: 朝倉書店
発売日: 2019/11/01
メディア: 単行本（ソフトカバー）

ということで、勉強してみたので、そのメモです。

EMアルゴリズム is 何？
問題設定
ざっくりな説明
- 流れ
- なんでこれでうまくいくのか？
感想

EMアルゴリズム is 何？

まずは定義を確認します。

EMアルゴリズム（英: expectation–maximization algorithm）とは、統計学において、確率モデルのパラメータを最尤推定する手法の一つであり、観測不可能な潜在変数（英語版）に確率モデルが依存する場合に用いられる。EM法、期待値最大化法（きたいちさいだいかほう）とも呼ばれる。その一般性の高さから、機械学習、音声認識、因子分析など、広汎な応用がある。 wikipedia

この場合のゴールは上の定義によれば、最尤推定をすることのようです。

尤度については、別の記事をご参照ください。

www.nogawanogawa.com

問題設定

定義を押さえたところで、少しずつ中身を見ていきます。

仮定するモデル

いま、ある試行の結果の分布が得られているとします。

f:id:nogawanogawa:20200202181842p:plain:w400

この観察結果から、裏側にある確率モデルを仮定し、モデルのパラメータを設定することを考えます。

横軸の値に対して、ピークが2つ確認できますので、おそらくこれは複数の分布が重ね合わさった混合モデルであると考えられます。

f:id:nogawanogawa:20200202182345j:plain:w450

混合モデルだと仮定したとき、この試行において結果が出力されるまでの過程は下記のようになると考えられます。

f:id:nogawanogawa:20200202183103j:plain:w500

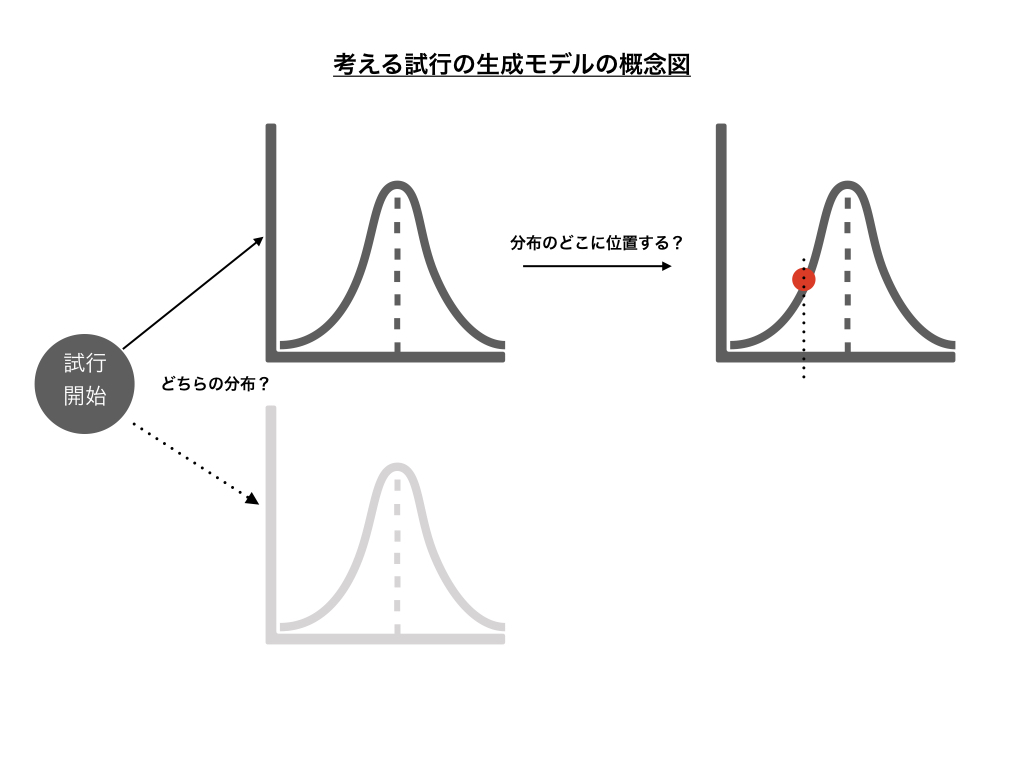
第一段階としてどちらの分布に従うかを選択し、第二段階として選択された分布の中で確率的にどこに位置するかが選択されるイメージです。この仮定のもとで考えるべきなのは、結果的に得られた分布から第一・第二段階の確率モデルを表現する関数を特定することになります。

第一段階で、分布はどうやって選んでいるでしょうか？
横軸となる観測パラメータではないので、このパラメータはいま持ち合わせていません。観測できないとすると、このパラメータは観測できない潜在変数として考えるのが適切です。つまり、結果として得られた謎の混合モデルの分布から、観測変数と潜在変数の同時分布を考える必要があります。そうすれば、潜在変数によって分布が選択され、同時に観測変数によって分布が形成されることを表現できます。

話をややこしくしているポイント

話がややこしくなってきているので、この場合でどこが難しいかを明確にします。

上のようにモデルを仮定すると、観測できない潜在変数を使って生成モデルを表現しないといけません。潜在変数がなければ通常の最尤推定やベイズ推定などによってモデルのパラメータを設定できますが、潜在変数がある点が普通と違う点です。

今回の混合モデルが、複数の正規分布の重ね合わせである混合ガウス分布であると考えると、正規分布のパラメータ $\mu , \sigma$ と重み $\pi$ で表現できる個別の正規分布を重ね合わせて表現されることになります。

$p(x|\mu , \sigma, \pi) = \sum_j\pi_j N(x|\mu , \sigma)$

ここで $N(x|\mu , \sigma)$ は正規分布を表すものとします。

この場合では、観測できない $\pi$ が通常より余計に含まれており、観測変数と潜在変数を同時に知ることができない不完全データになっています。そのため、基本通りに最尤推定やベイズ推定ができず、今回話がややこしくなっています。

モデルを特定する方針

じゃあどうするのか？ってことで、もうちょっと考えてみます。

要するに、どの山を選択するかというパラメータが観測できないから問題になっているわけです。ということで、これを確率変数として扱うことで尤度の期待値で考えれば先に進めそうです。

これは、本来やりたい「尤度の最大化」とは異なりますが、期待値を使用することで「尤度の期待値の最大化」なので、やりたい方向性としてある程度近似できているだろうとしています。

ざっくりな説明

さて、本題のEMアルゴリズムの話に移ります。まずは、数式は使わず直感的に何をやるのか見ていきます。

上で書いたように、混合モデルによって尤度の最大化が通常の方法では困難になるため、潜在変数を確立変数として取り扱うことで尤度の期待値を最大化するというアプローチを考えることで、近似的にパラメータを推定するアプローチがEMアルゴリズムになります。

混合モデルにおいて、重ね合わせのもとになる全ての分布が正規分布である混合ガウス分布では、対数尤度*1の期待値であるQ関数は次のようにおいています。

$Q(\theta, \hat{\theta)} = \mathbb{E}_{p(z|x, \hat{\theta})}[log p(x,z|\theta)] = \int p(z|x, \hat{\theta}) log p (z,x| \theta)dz$

要するに、直接尤度について解くわけじゃないってことです。

この時、観測変数と潜在変数の両者が結果に影響を与えていると考えられますが、潜在変数は観測できていないのでこれも同時に推定する必要があります。

潜在変数について考えると、下図のような点で潜在変数の負担率を考えます。

f:id:nogawanogawa:20200202193442j:plain:w500

重ね合わせる前のそれぞれの分布が得られれば、負担率 $r_{ij}$ は下記のように求めることができます。

$r_{ij} = \mathbb{E}_{p(z^{(i)}|x^{(i)}, \hat{\theta})}[z_{ij}$ ]

逆に、分布のパラメータは負担率が決定されれば、Q関数は負担率 $r_{ij}$ を使って次のように求めることができます。

$Q(\theta, \hat{\theta)} = \sum_{i=1}^{n} \sum_{j=1}^{k} r_{ij}(log \pi_j + log N(x^{(i)} | \mu_{j}, \sigma_{j}^{2}))$

このように、分布のパラメータと負担率は、一方が他方さえ決定されれば推定できるという状況になっています。そのため、一方を仮定した状態で他方を推定し、推定した値を使用してまた仮定した値を更新する、といったことを繰り返していけば、最終的に互いに妥当な値に収束することが期待されます。

流れ

EMアルゴリズムではEステップとMステップを繰り返して、徐々にパラメータを適切な値に近づけていきます。イメージはこちらのスライドを非常に参考にさせていただきました。

数式を使わずイメージで理解するEMアルゴリズム from 裕樹奥田

Eステップ(期待値計算)
- 分布のパラメータ $\theta$ を固定し、負担率を計算し
Mステップ(最大化)
- 負担率を固定して、対数尤度が最大化するパラメータ $\theta$ を求める

なんでこれでうまくいくのか？

これでパラメータが定まるのは、変分下界とKLダイバージェンスを考えると説明できるそうです。対数尤度はKLダイバージェンスと変分下界の和、変分下界はエントロピーとQ関数の和と求めることができます。

f:id:nogawanogawa:20200202195900j:plain:w500

Eステップ・Mステップは、やることは違えど、どちらも変分下界を拡大する行為になります。

f:id:nogawanogawa:20200202195918j:plain:w500

f:id:nogawanogawa:20200202195943j:plain:w500

そのため、各ステップで値が変動しなくなる方向（収束）に向かっていくようです。これを無限回繰り返せば対数尤度と変分下限は一致するように変分下界が拡大していくため、負担率とパラメータをQ関数が拡大する方向に徐々に更新することで、最終的にパラメータが定まるようです。

一点注意としては、必ずしもEMアルゴリズムで対数尤度が最大化はせず、局所最適解に収束する可能性があります。多数のEMアルゴリズムによる探索を行い、求めた収束値を比較して、最終的なパラメータを設定する必要があります。

感想

わかったようなわかってないような...って感じだった最尤推定ですが、EMアルゴリズムを勉強したことでちょっと理解できた気がします。

いつものように導出はガッツリ端折ってますし、テクニック的な部分もかなり端折っています。実際の教科書ではもうちょっときちんと数学的に説明されていますので、正確に知りたい方はこちらの本がわかりやすかったので、こちらを読んでいただければ大丈夫かと思います。

しくみがわかるベイズ統計と機械学習

作者:手塚太郎
出版社/メーカー: 朝倉書店
発売日: 2019/11/01
メディア: 単行本（ソフトカバー）

まあ、自分は数式レベルでなんかすることはないので、このへんで。

*1:最尤推定において、尤度を最大にするパラメータは、尤度関数の対数も最大になるため、求めるパラメータは同一になり、式展開の簡便さから対数尤度が使われます。