検索の評価に関するあれこれ - Re:ゼロから始めるML生活

f:id:nogawanogawa:20210919130054p:plain:w400

以前、こちらの書籍を読んでました。

情報検索 :検索エンジンの実装と評価

森北出版

Amazon

この中で、検索の評価に関する話がありました。

検索の文脈でアルゴリズムを評価したくなるかもしれません。このときの評価の方法がいまいちわかっておらず、いい機会だったので勉強してみたので今回はそのメモです。

問題設定
ざっくりとした評価に関するイメージ
古典的な評価指標
nDCG
- 余談 : 2つのnDCG
- やってみる
RankEff
参考文献
感想

問題設定

まずは、ランキングを評価するということについてもう少し考えてみます。

ベースライン

いま、とある検索窓に検索ワードを入力した結果、下記のような検索結果が得られたとします。

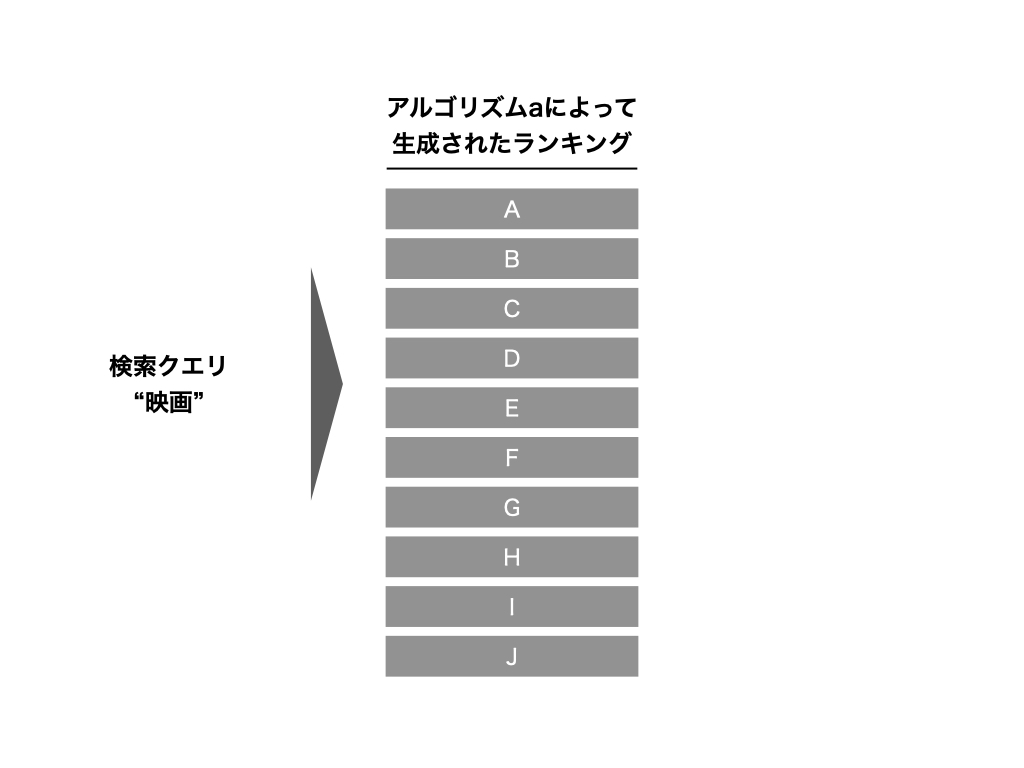
f:id:nogawanogawa:20210925090021j:plain

この表示された結果に対して、ユーザーは何らかのアクションを起こします。

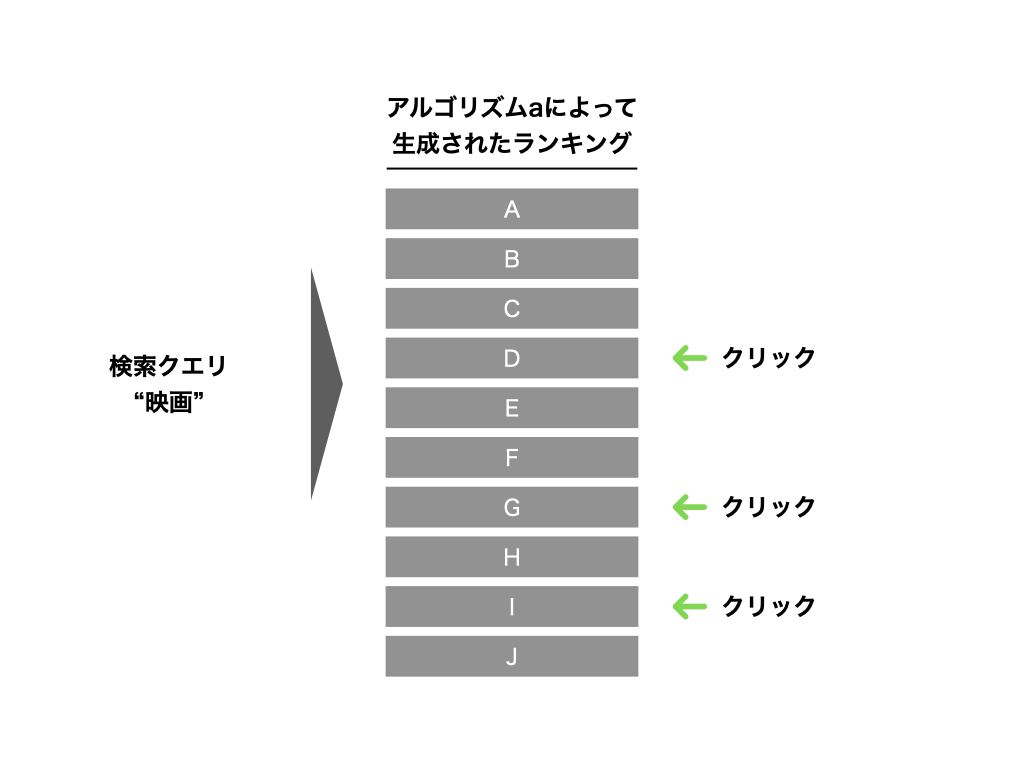
f:id:nogawanogawa:20210925090038j:plain

ここまでをベースラインにとして考えます。

比較対象

次に、ベースラインの検索アルゴリズムに対して、何らかの修正を行ったとします。そのとき、下記のような結果が出力されたとします。

f:id:nogawanogawa:20210925111954j:plain

この表示された結果に対しても、ユーザーは何らかのアクションを起こします。

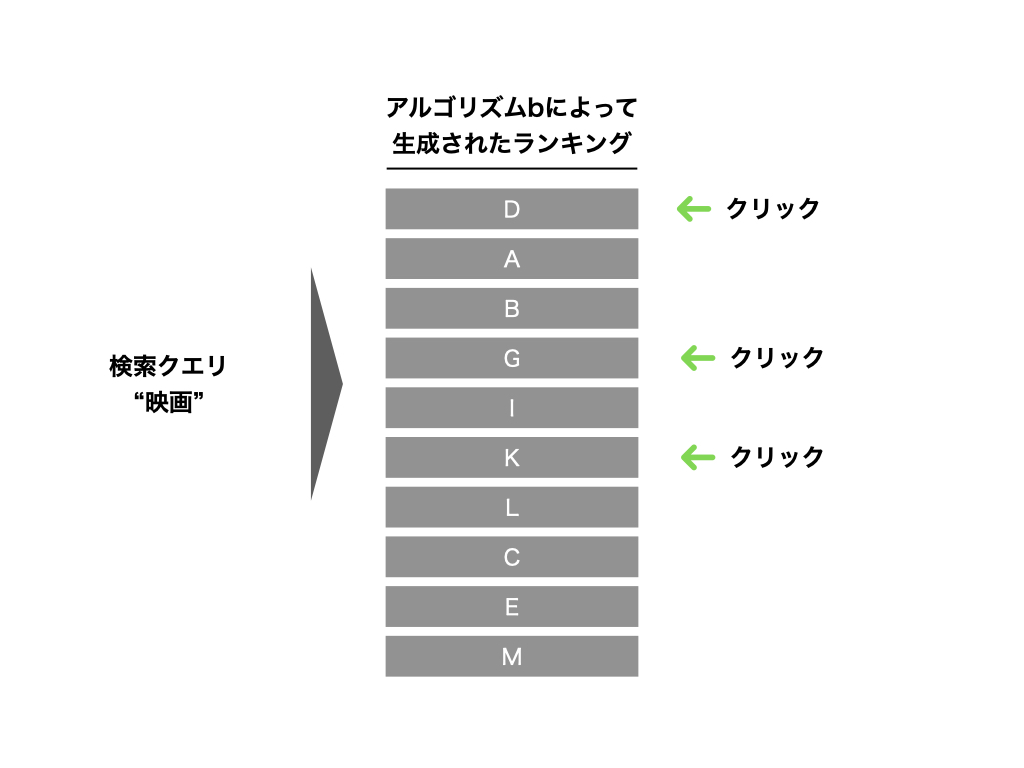
f:id:nogawanogawa:20210925112002j:plain

問題となるポイント

ここまでで、ベースラインと比較対象の2種類の検索結果とそのときのユーザーの応答が得られていることを確認しました。

さて、この2つのランキングアルゴリズムのうち、どちらのほうが優れていると考えられるでしょうか？

こんな感じのことを考えることが、今回やりたいことになります。

ざっくりとした評価に関するイメージ

この辺りはあまり書籍などで言及されないので、ちょっと自分のイメージを残しておきます。

情報検索の文脈では、情報要求を効率良く満たすことができるアルゴリズムが優れていると考えられます。すなわち、ユーザーが検索クエリを発行してから欲している情報に到達するための労力や時間が少ないほど良いと考えます。

この前提をもとに考えると、検索結果のうち、真にユーザーが欲しかった情報はランキングの1ページ目に表示されるべきだし、ランキング上位にあればあるほどスクロールする労力や時間が短縮されるため、良い検索アルゴリズムであると考えられます。

そのため、ユーザーが真にほしかった情報を上位に表示されている度合いを評価してあげれば、ランキングアルゴリズムを比較・評価できそうです。

古典的な評価指標

まずは古典的な評価指標を用いることを考えます。

PrecisionとRecall

もっとも単純な評価指標としては、Precision（適合率）とRecall（再現率）かと思います。検索結果によって得られたドキュメントの集合をRes、情報要求に適合するドキュメントの全体をRelとすると

$\displaystyle{ precision = \frac{|Res \cap Rel|}{|Res|} }$

$\displaystyle{ recall = \frac{|Res \cap Rel|}{|Rel|} }$

のように定義されます。どちらも高ければ高いほど、関連あるドキュメントを多く提示できていることを意味し、高いほど良いということになります。検索の場合には、検索結果すべてをユーザーが閲覧することは稀であるので、ランキングの上位k件（top@k）でこれらの値を見るかと思います。特に、ドキュメントの数が膨大になりがちな現代ではRecallではなく、検索結果top@kにおけるPrecisionのほうが重要な指標と考えられたりします。

平均適合率

上で紹介したように、適合率が結構重要視されたりするのですがこの値はどこまでkの値を取るかによって評価が変わったりします。これをkの値によらず判断する指標として、平均適合率（AP）が使われたりします。

$\displaystyle{ AP=\frac{1}{|Rel|} \sum_{i=1}^{|Res|} relevant(i) \cdot P@i }$

意味してるところはkの値を変化させていったときのPrecisionの平均ですね。これならkの大きさに関する議論はなくなりますね。

逆数順位

場合によっては、ユーザーの情報要求を満たすドキュメントがただ一つに定まる状況もあります。そのような場合には、求めるアイテムがランキングの1位に近いところに出現しているかにフォーカスして評価することが求められたりします。

そういうときに逆数順位（reciprocal rank(RR)）が使われたりします。

$\displaystyle{ RR = \frac{1}{min \{ k|Res[k] \in Rel\} } }$

幾何平均適合率

上で紹介した平均適合率や逆数順位をさまざまなケースを行ったときに、平均を取りたくなることがあります。

これを算術平均で行ってしまうと、情報要求を満たすドキュメントがResに含まれないという状況についてのペナルティが小さくなってしまいます。言い換えれば、ユーザーがどれだけ頑張ってスクロールしてもお目当てのドキュメントが表示されることがなかったということなので、単純にランキングの順位が低いよりペナルティが大きくなっていてほしい場合があります。

そんなこんなで、幾何平均適合率(geometric mean average precision(GMAP))が取られることがあるようです。

$\displaystyle{ GMAP(AP_1 , ... , AP_n) = \sqrt[n]{\prod_{i=1}^{n}(AP_i + \epsilon)} - \epsilon }$

これにより、すべてのケースでとにかく適合していたほうが値が良くなるように指標を設定できます。

統計的手法の使用

シンプルにRecallやPrecisionを使うのではなく、もっと統計的に見たい場合もあったりします。特にドキュメントの全体集合が変化する場合の普遍的な検索エンジンの性能を議論するときには、指標を統計的に評価してあげる必要があったりします。

この辺は、統計の知識があれば評価できると思うのでこのへんで。必要なら仮説検定で有意差見て判断しましょう、ってことだと思ってます。

nDCG

次はnDCG (normalized Discounted Cumulative Gain)を見ていきます。

検索結果として出力されるアイテム集合にゲイン（利得）を考えます。検索によって表示されるアイテムは、必要/不要の2値ではなく、多くの場合グラデーションがあったりします。例えばECサイトでの検索を考えると、

商品の詳細ページを閲覧する：1
欲しい物リストに追加する：3
カートに入れる：5
商品を購入する : 10

のように重み付けできたりします。こんな感じで利得にグラデーションをつけることができます。

検索では、何らかの指標に基づいてアイテムの並べ替えが行われ、本来的にはゲインが大きなものほどランキングの上位に位置することが期待されます。しかし実際にそのゲインの情報が得られるのは検索結果を表示したずっとあとになり、検索結果は必ずしも真のゲインに基づいてソートされているとは限りません。このズレについて評価するのがnDCGと考えることができます.。

表示したアイテムについて、真のゲインについて順位による減衰を考慮して足し上げ、それを対象順位のアイテム数で平均することでランキングの性能指標として考えます。

式としては下記のように記述されます。

$\displaystyle{ DCG = r_1 + \sum_{i=2}^{n} \frac{r_i}{log_2 i} }$

これを、理想的なランキングの状態と実際に出力されたランキングの状態とでスコアの比率をとったものがnDCGになります。

$\displaystyle{ nDCG = \frac{DCG_{pred}}{DCG_{true}} }$

理想的なランキングな状態に対してどれだけ近しいか、という意味合いでしょうかね。

これによって、ランキングの順位まで考慮した評価が可能になりました。

余談 : 2つのnDCG

上では、観測範囲内では一般的なnDCGの定義を書きました。しかし、こちらの記事によれば実はnDCGの定義には2種類あるそうです。

違いが出るのはDCGの計算式で、上とは異なるDCGの定義では下記のようになるそうです。

$\displaystyle{ DCG = \sum_{i=2}^{n} \frac{2^{r_i}-1}{log_2 (i+1)} }$

おおきな違いは利得の計算に2のべき乗を使用している点でしょうか。

やってみる

実際使うときはどんな感じで使うかを最後に書いてみたいと思います。まあこんな有名な関数なんだから、どっかのライブラリに入ってるんだから一発だろ、と思って探してみると、ありました。

scikit-learn.org

いや、あるんですがこれちょっと癖があるようで、こんな質問もあります。

stackoverflow.com

なんか確率分布がどうたらこうたら言っていてコレジャナイ感がすごいので、今回は普通に関数を自作してやっていきます。

def dcg(gain, k=None):
    """ calc dcg value """ 
    if k is None:
        k = gain.shape[0]

    ret = gain[0]
    for i in range(1, k):
        ret += gain[i] / np.log2(i + 1)
    return ret


def ndcg(y, k=None, powered=False) -> float:
    """ calc nDCG value """

    dcg_score = dcg(y, k=k)
    print("pred_sorted_scores : {}".format(dcg_score))

    ideal_sorted_scores = np.sort(y)[::-1]
    ideal_dcg_score = dcg(ideal_sorted_scores, k=k)
    print("ideal_dcg_score : {}".format(ideal_dcg_score))
    
    return dcg_score / ideal_dcg_score

計算結果があってるかどうかわからないので、他のブログの記事に書いてある値の通りになるか確認してみます。

まずはこちらの記事を参考に確認します。

pred = np.array([3.0, 4.3, 0.0, 2.5, 1.0])
ndcg(pred)
#pred_sorted_scores : 8.980676558073394
#ideal_dcg_score : 9.377324383928643
#0.9577013858521259

別の記事でも確認してみます。

pred = np.array([3, 3, 3, 3, 3, 0, 0, 0, 0, 5])
ndcg(pred)
#pred_sorted_scores : 12.189968913254459
#ideal_dcg_score : 13.845377356638178
#0.8804360184094201

pred = np.array([5, 0, 0, 0, 0, 3, 3, 3, 3, 3])
ndcg(pred)
#pred_sorted_scores : 10.078664600376822
#ideal_dcg_score : 13.845377356638178
#0.7279443774455593

なんだか正しい結果を返しているようです。

ということで、冒頭の例について確認してみたいと思います。

まずはAのランキング。

pred = np.array([0, 0, 0, 1, 0, 0, 1, 0, 1, 0])
ndcg(pred)
#pred_sorted_scores : 1.1716720638937508
#ideal_dcg_score : 2.6309297535714578
#0.4453452481212085

次にBのランキング。

pred = np.array([1, 0, 0, 1, 0, 1, 0, 0, 0, 0])
ndcg(pred)
#pred_sorted_scores : 1.8868528072345416
#ideal_dcg_score : 2.6309297535714578
#0.7171809907403115

top@10という枠組みではありますが、この場合ではBのランキングが良さそうということが数字から読み取れました。

RankEff

すべてのドキュメントに関する関連性が判明していれば良いですが、新規に追加されたドキュメントなどは関連性が評価されず不明になっている場合もあります。そういったケースは一般的に関連性がないものとして取り扱われる場合が多いですが、この追加されたドキュメントが実は関連性があるケースも大いにあり、そういったケースが問題になることがあります。

こうした場合に、ランク有効性指標(rank effectiveness measure (RankEff))が使われることがあります。

$\displaystyle{ RankEff = \frac{1}{|Rel|} \cdot \sum_{i=1}^{|Res|} relevant(i) \cdot (1 - \frac{|Res [ 1..i] \cap Non|}{|Non|}) }$