Re:ゼロから始めるML生活

どちらかといえばエミリア派です

確率分布について最近見かけたもののメモ

統計 R

f:id:nogawanogawa:20200202130118p:plain
　

最近ベイズとかを勉強していく中で、いろんな確率分布を見かけました。 正直どれがどれだかわかんなくなってきて、だんだん全部いっしょに見えてきました。 そこで、最近勉強しててよく見かける確率分布だけでも理解のために整理しようと思ったのでそのメモです。

結論

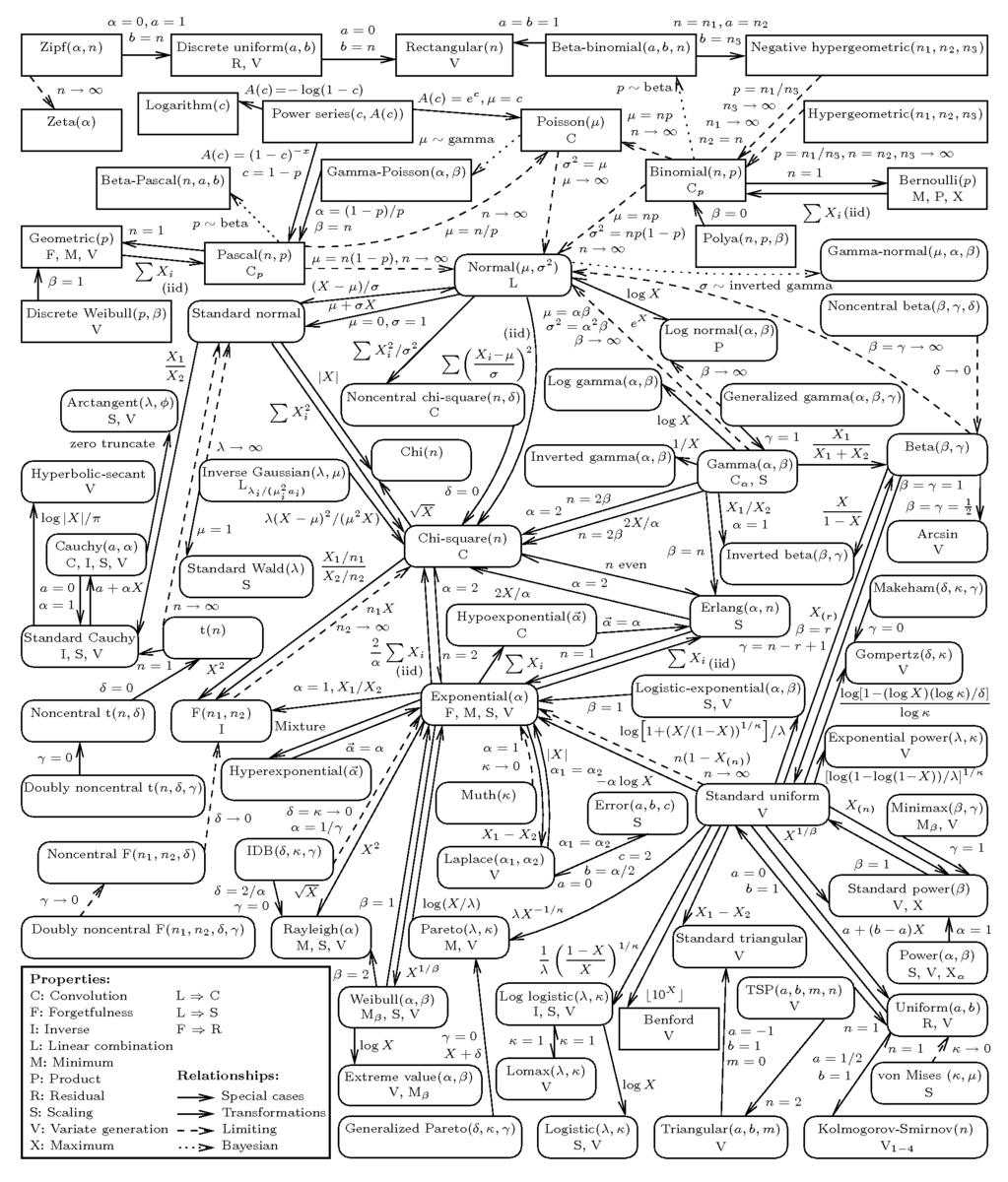
とりあえずこちらのサイトで網羅されてるようなので、これを全部マスターできれば確率分布マスターです！！

www.math.wm.edu

http://www.math.wm.edu/~leemis/2008amstat.pdf

確率分布

上のサイトを紹介しただけで目的は達成したと思いますので、あとはのんびり見ていきます。

確率分布は扱う事象が連続的な値か、離散的な値かで、

  • 連続確率分布
  • 離散確率分布

に大別できます。 連続確率分布は、連続性を持つ数値に関する確率分布、離散確率分布は離散性（特定の飛び飛びの値しか取らない）を持つ数値に関する確率分布と成っています。

連続確率分布(Continuous)

連続確率分布は、ある分布に対して連続確率分布と仮定して式展開を行ったりします。 事前確率として仮定されたりするので、、、なんていう理解です。

ということで、どんなケースで分布に従うかを知っとくと得しそうです。

正規分布・Gauss分布

正規分布は平均を中心にして左右対称、標準偏差によって裾の広さを表した分布になります。 正規分布の確率密度関数はこのようになります。

f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} exp(- \frac{(x-\mu)^2}{2 \sigma^2})

平均2、標準偏差0.5の正規分布はこんな感じ。

f:id:nogawanogawa:20200223150317p:plain:w500

適合するケース

パスカルの三角形で考えられる分布は正規分布として仮定できるようです。

www.albert2005.co.jp

標準正規分布

標準正規分布は、正規分布のうち平均\muが0、標準偏差\sigmaが1のものを指します。

f(x) = \frac{1}{\sqrt{2 \pi }} exp(- \frac{x^2}{2})

標準正規分布はこんな感じになります。

f:id:nogawanogawa:20200223150514p:plain:w500

適合するケース

正規分布を平均0、標準偏差1に変形しただけなので、基本的にはこちらもパスカルの三角形が適用できるケースでは正規分布とみなすことができそうです。

指数分布

指数分布は、次に何かが起こるまでの期間が従うときの分布を表します。

f(x) = \lambda e^{-\lambda x}

図にするとこんな感じになります。

f:id:nogawanogawa:20200223152023p:plain:w500

期間が進めば進むほど減少する形になります。

適合するケース

指数分布は

  • 機械が故障してから次に故障するまでの期間
  • 災害が起こってから次に起こるまでの期間

と言った、一定期間に〇〇回事象が発生することが経験的にわかっている場合に使用されるようです。

ベータ分布

ベータ分布は下記のような式で表されます。

f(x) = \frac{\Gamma(\beta - \gamma) x^{\beta -1} (1-x)^{\gamma-1}}{\Gamma(\beta) \Gamma(\gamma)}

このように同じベータ分布であってもパラメータ次第で多様な形状を取ることができる特徴があります。

f:id:nogawanogawa:20200223153256p:plain:w500

f:id:nogawanogawa:20200223153310p:plain:w500

適合するケース

珍しいらしく、多様な形状を表現できる点がある一方で、具体的なケースとなるとなかなか登場しないようです。

www.ntrand.com

ガンマ分布

ガンマ分布は指数分布を一般化した分布と言えます。

f(x) = \frac{x^{\alpha-1}e^{-\frac{x}{\beta}}}{\beta^{\alpha} \Gamma(\alpha)}

形状としては指数分布とそんなに変わりません。

f:id:nogawanogawa:20200223153648p:plain

適合するケース

wikipediaによれば

信頼性工学における電子部品の寿命分布や通信工学におけるトラフィックの待ち時間分布

などがこの分布に従うようです。

ラプラス分布

ラプラス分布は両側指数分布とも言われます。

f(x) = \begin{cases} \frac{1}{\alpha_1 + \alpha_2} e^{\frac{x}{\alpha_1}} (0 > x) \\ \frac{1}{\alpha_1 + \alpha_2} e^{-\frac{x}{\alpha_2}} (x \geq 0) \\ \end{cases}

f:id:nogawanogawa:20200223160751p:plain:w500

適合するケース

形状の特徴から、正規分布よりデータ分布の頂点が鋭い際に使用されるようです。

(追加)ディリクレ分布

これだけ上のサイトに載ってなかったです。 あまりこの手の話はよくわからないんですが、何かの分布の拡張という位置づけだから載せてないとかなんですかね？

とはいうものの、少なくともここ最近の私の観測範囲では頻出の分布なのでこれも入れときます。

f(x) = \frac{ \Gamma (\sum^{k}_{j=1}\alpha_j)}{\prod^{k}_{j=1} \Gamma (\alpha_j) } \prod^{k}_{j=1} x^{\alpha_{j-1}}_{j}

離散確率分布(Descrete)

離散確率分布は、

実際の試行を考えるときに、それが従うはずと想定する対象

という意味合いが強い印象です。

連続性がないような試行の結果に対して、ヒストグラムはこんな感じになるだろう、という位置づけで使われている気がします。

ということで、離散確率分布については、どのような問題設定のときに分布に従うかを知っておくと役に立ちそうです。

ベルヌーイ分布 (Berunulli Distribution)

ベルヌーイ分布はベルヌーイ試行１回行った際の成功するかどうかについての確率分布です。

p(x|\mu)=\mu^{x}(1-\mu)^{1-x}

よく出てくる設定

コインを1回投げるときなどに使われる分布です。 発生する事象が、2通りしかなく、必ずどちらかの状態を持ちます。(ベルヌーイ試行)

このコインを1回投げて表が出るについての分布がベルヌーイ分布の例と言えます。

二項分布 (Binomial Distribution)

二項分布はベルヌーイ試行をm回行って、成功する回数rが従う確率分布です。

p(r|m,\mu) = \frac{m!}{r!(m-r)!} \mu^r (1-\mu)^{m-r}

f:id:nogawanogawa:20200223172349p:plain:w500

よく出てくる設定

コインを投げるときなどに使われる分布です。 発生する事象が、2通りしかなく、必ずどちらかの状態を持ちます。(ベルヌーイ試行)

このコインをm回投げてr回表が出るについての分布が二項分布の例と言えます。

Poisson分布

単位時間あたりに平均\mu回起こる現象が、単位時間にx回起きる確率がPoisson分布を表します。

f(x) = \frac{\mu^{x} e^{-\mu}}{x!}

f:id:nogawanogawa:20200223180826p:plain:w500

よく出てくる設定

放射性物質から、単位時間当たりに発生する放射線の量などがあるそうです。

使ったコード

なにかで確率分布の絵が必要になることがあるかも知れないので、残しときます。 いざ作ろうとすると調べたりしてめんどくさかったりするので。

github.com

一応これでパパっとグラフのイメージは作れるかと思います。

感想

自分の勉強で出てくるような超基本的なところは押さえられたかと思うので、今回はこれでよし。 グラフをいちいち描画するのがめんどくさかったので描画の仕方を記録に残したかったという意味では目的達成ということで。 あとは、必要になったら都度探しに行けばいいと思います。

それにしても、このマップすごいですね。 こんなのあるんだ… 困ったら上のマップを見るのが手っ取り早そうですね。