この前はベイズモデリングの中でも一般化線形モデルを勉強していました。
今回は、階層ベイズを使ったモデリングである一般化線形混合モデルについて勉強していきたいと思います。
今回も主に参考にさせていただいたのはこちらです。

実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門 (KS情報科学専門書)
- 作者:馬場真哉
- 出版社/メーカー: 講談社
- 発売日: 2019/08/23
- メディア: Kindle版
混合モデル
一般化線形混合モデルについて触れる前に混合モデルについて確認します。
この前の一般化線形モデルでは、モデルにおいて線形予測子は通常の変数でした。 つまり、線形予測子は変数さえ決まってしまえば一意に効果を導くことができる、固定効果を表します。 混合モデルでは、この線形予測子に確率変数が組み込まれます。 これによって、説明変数の組み合わせだけで表現しきれない事象について、ランダム効果を混ぜ合わせて事象を表現できる範囲を広げることができます。
階層ベイズ
混合モデルを作る際に、階層ベイズの考え方が出てきます。 通常のベイズの定理では、事後分布は事前分布と尤度の積に比例します。
このときの事前分布は、正規分布を例にすると、平均と分散といったパラメータは実数となっています。 階層ベイズでは、この事前分布のパラメータが確率変数に置き換えることができます。 イメージとしては、段階的に確率変数を経由して、事象が表現されていくイメージですかね。
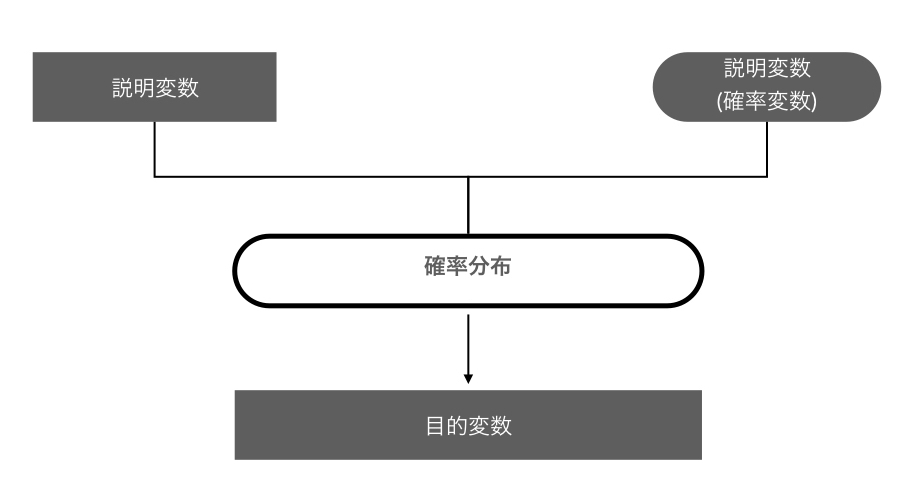
この階層ベイズによって、実際には測定されていない(あるいは測定できない)値を確率変数として表現して考慮することができるようになり、モデリングする際の自由度が広がります。
一般化線形混合モデル
この前やった一般化線形混合モデルはこのように考えるモデルでした。
それに対して今回扱う一般化線形"混合"モデルは、こんな感じに線形予測子にも確率変数が使用されて、階層ベイズの構造をとったモデルと考えられます。
モデリングしてみる
ざっくり概要を紹介したところで、本題に入ります。
ランダム切片モデル
ランダム切片モデルでは、「グループごとにランダム効果が異なる」と仮定してモデリングを行います。
問題設定
この例では、esophのデータを使用します。
下記のようなデータが与えられていたとします。
データでは、食道がんの症例が、年齢・喫煙・飲酒のデータと共に与えられています。

この時、年齢・喫煙・飲酒と食道がんの相関関係を確認したいとします。
考え方
ランダム切片モデルでは、グループごとにランダム効果を別々のランダム効果を仮定します。 今回では、年齢層によってランダム効果を分けたいと思います。
そうした時に線形予測子は、アルコール摂取量(alcgp)、タバコ(tobgp)、年齢(agegp)を用いて、
と考えてみます。 この時、年齢については確率変数として取り扱い、ここでグループ化します。
brmで記述する際には
(1|agegp)
のように表現することでランダム性を記述することができるようです。
そうしたときに、実際にこのモデルが妥当かどうかはMCMCサンプリングで確認してみます。
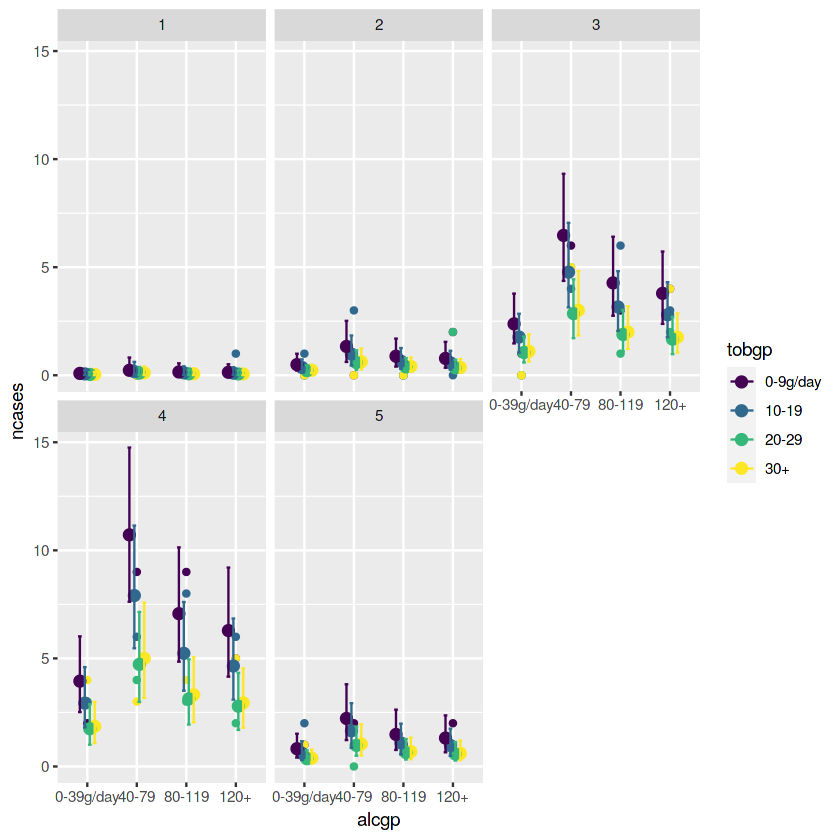
年齢ごとにグラフが分けられています。 これによって、年齢毎に考えることができます。
グラフから、若い人は飲酒しようがタバコを吸おうがあまり影響がないことが分かり、逆に40~60代の方は飲酒を多少してタバコはほとんどやらない人のところが非常にがんの確率が高くなってます。 (なんでだろ。。。外れ値が入っちゃってるからですかね?)
ランダム係数モデル
ランダム係数モデルは、ランダム効果に応じて他の説明変数の固定効果の強さが増減するモデルとなっています。 要するに、ランダム性が他の変数自体に影響を与えちゃうパターンですね。
問題設定
今回はCO2のデータを使います。 (※似た名前でco2という時系列データもありますのでご注意ください)
下記のようなデータが与えられていたとします。 植物の二酸化炭素の吸収率を植物の生息地・種類・周囲の二酸化炭素濃度によって調査したデータです。
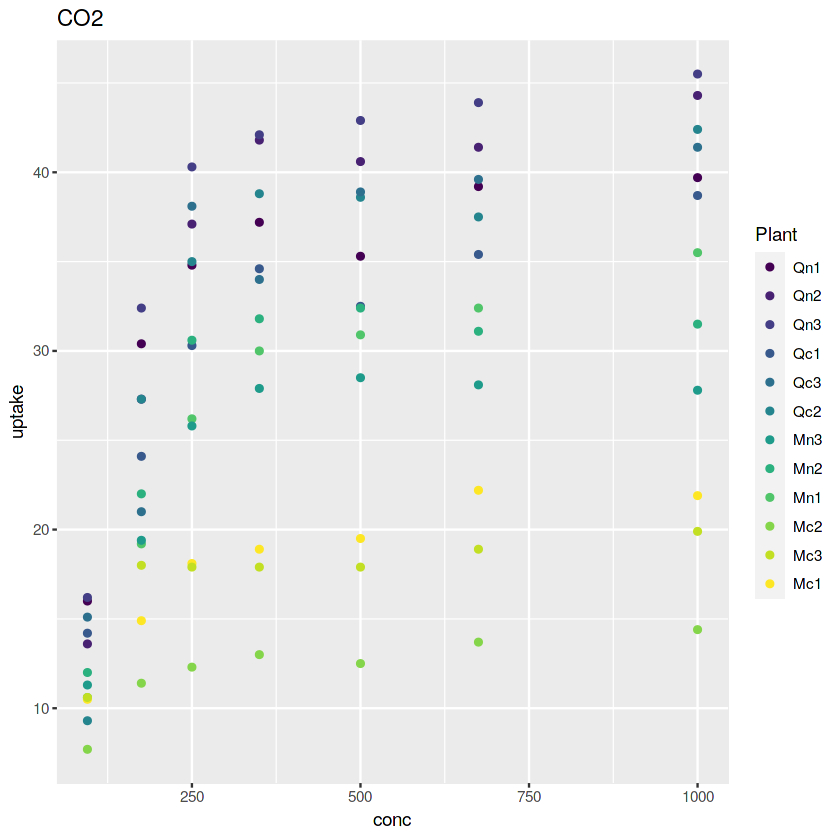
このときの二酸化炭素の吸収率を植物の生息地・種類・周囲の二酸化炭素濃度の関係をモデル化したいものとします。
考え方
ランダム係数モデルでは、ランダム性が変数に影響を与えるとしました。 この場合では、産地と植物の種類が相関がありそうなので、それを踏まえて考えてみます。
ランダム係数モデルはbrm内で
(影響を受ける変数|因子)
と指定します。この時、
(影響を受ける変数||因子)
だと、因子の影響で変数が変化することを表現できます。 また、
(影響を受ける変数|因子)
因子の影響とそれによって影響を受ける変数の影響を同時に受ける、係数同士の相関を表現する事ができます。
そのようにしてやってみるとこんな感じになりました。
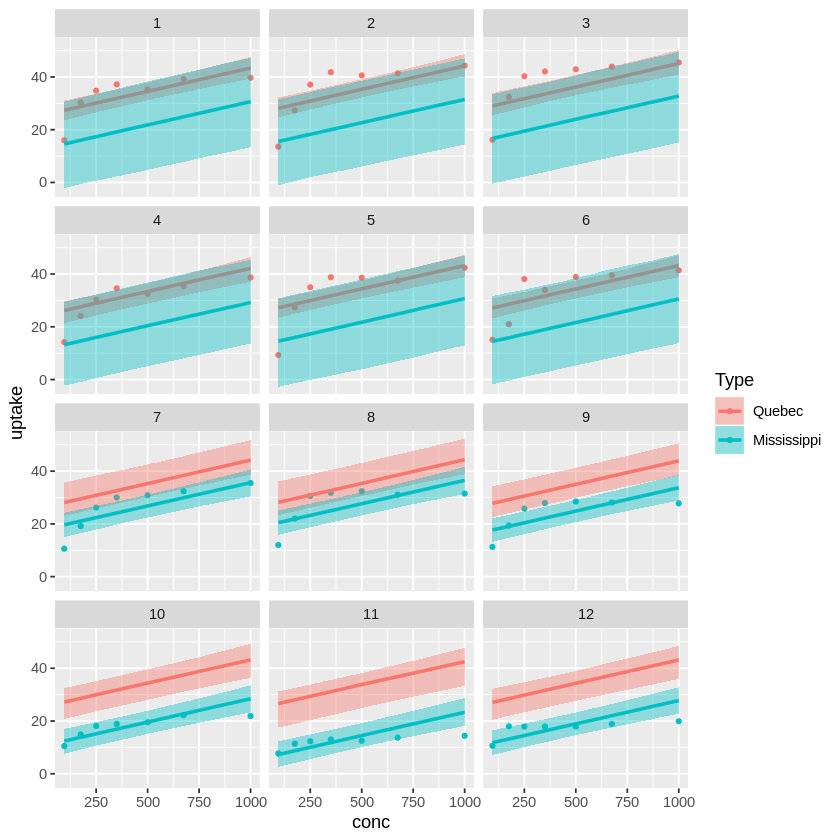
評価とかあんまりわかりませんが、よくなさそうです。
ちなみに、ランダム切片モデルと思ってやってみるとこんな感じになりました。

なんともよくわかりませんが、こっちの方がよく捉えている気がします。
モデリングに使えることは分かりましたが、実施したモデリングが正しいかは別問題ですね。 この辺の妥当性については、評価の仕方をちゃんと勉強しないといけないですね。
参考
https://prs.ism.ac.jp/~nakama/Rjp/datasets-manual.pdf
使ったコード
感想
前回と比較して考えるモデルは難しくなった気がします。 その分、より複雑な内部構造を考えても対応できる強力な考え方だなと感じます。
こちらの本では状態空間モデルがこのあと紹介されますが、状態空間モデルについては別に積ん読がありますのでそちらできちんと勉強したいと思います。

実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門 (KS情報科学専門書)
- 作者:馬場真哉
- 出版社/メーカー: 講談社
- 発売日: 2019/08/23
- メディア: Kindle版
こちらの本は、理論重視というよりはモデリングをどうやってやるかという視点で書かれているので、より実務で使用することを想定したような本でした。 どちらかといえばコードを書きながら、モデルリングとはどうやってやるかに重心があるので、難しい数式の証明とかにアレルギーのある方は、この本などから入るとモデリングを考えながら入門できて良いかと思いました。
あとは、いろいろ叩けばモデリングはできそうですが、その評価とかセオリーとかは別途やらないといけないですね。 まあ、Rの勉強と思えば、こんなもんですかね。